Menu Close

Solve-this-equation-by-reducing-it-from-non-homogeneous-equation-to-homogeneous-equation-dy-dx-x-y-3-x-y-5-

Tinku Tara 0 Comments
Pin




Question Number 6651 by Tawakalitu. last updated on 08/Jul/16
Solve this equation by reducing it from non homogeneous equation to homogeneous equation (dy/dx) = ((x + y + 3)/(x − y −5))
$${Solve}\:{this}\:{equation}\:{by}\:{reducing}\:{it}\:{from}\:{non}\:{homogeneous} \\ $$$${equation}\:{to}\:{homogeneous}\:{equation}\: \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{x}\:+\:{y}\:+\:\mathrm{3}}{{x}\:−\:{y}\:−\mathrm{5}} \\ $$
Commented by prakash jain last updated on 09/Jul/16
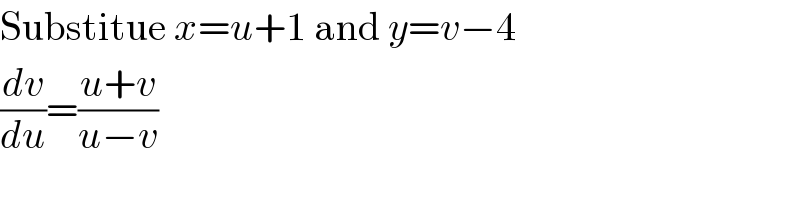
Substitue x=u+1 and y=v−4 (dv/du)=((u+v)/(u−v))
$$\mathrm{Substitue}\:{x}={u}+\mathrm{1}\:\mathrm{and}\:{y}={v}−\mathrm{4} \\ $$$$\frac{{dv}}{{du}}=\frac{{u}+{v}}{{u}−{v}} \\ $$$$ \\ $$
Answered by nburiburu last updated on 09/Jul/16
(x+y+3)dx+(−x+y+5)dy=0 { ((x+y+3=u+v)),((−x+y+5=u−v)) :} { ((u=y+4)),((v=x−1)) :} (u+v) dv+(u−v)du=0 homogeneus function u=t.v du=v.dt+t.dv v(t+1)dv+v(t−1)(vdt+tdv)=0 (t+1+t^2 −t)dv+(t−1)vdt=0 (1/v)dv =((1−t)/(1+t^2 )) dt ln v = atan(t)−(1/2)ln(1+t^2 )+c t=(u/v)=((y+4)/(x−1)) ; v=x−1 ln(x−1)=atan(((y+4)/(x−1)))−(1/2)ln((((x−1)^2 +(y+4)^2 )/((x−1)^2 )))+c and this should define implicitly y=f(x)
$$\left({x}+{y}+\mathrm{3}\right){dx}+\left(−{x}+{y}+\mathrm{5}\right){dy}=\mathrm{0} \\ $$$$\begin{cases}{{x}+{y}+\mathrm{3}={u}+{v}}\\{−{x}+{y}+\mathrm{5}={u}−{v}}\end{cases} \\ $$$$\begin{cases}{{u}={y}+\mathrm{4}}\\{{v}={x}−\mathrm{1}}\end{cases} \\ $$$$\left({u}+{v}\right)\:{dv}+\left({u}−{v}\right){du}=\mathrm{0} \\ $$$${homogeneus}\:{function} \\ $$$${u}={t}.{v} \\ $$$${du}={v}.{dt}+{t}.{dv} \\ $$$${v}\left({t}+\mathrm{1}\right){dv}+{v}\left({t}−\mathrm{1}\right)\left({vdt}+{tdv}\right)=\mathrm{0} \\ $$$$\left({t}+\mathrm{1}+{t}^{\mathrm{2}} −{t}\right){dv}+\left({t}−\mathrm{1}\right){vdt}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{v}}{dv}\:=\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$${ln}\:{v}\:=\:{atan}\left({t}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+{c} \\ $$$${t}=\frac{{u}}{{v}}=\frac{{y}+\mathrm{4}}{{x}−\mathrm{1}}\:;\:{v}={x}−\mathrm{1} \\ $$$${ln}\left({x}−\mathrm{1}\right)={atan}\left(\frac{{y}+\mathrm{4}}{{x}−\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}+\mathrm{4}\right)^{\mathrm{2}} }{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right)+{c} \\ $$$${and}\:{this}\:{should}\:{define}\:{implicitly}\:{y}={f}\left({x}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 09/Jul/16
Wow thanks why do we have tan^(−1) (t) i thought ((1 − t)/(1 + t^2 )) should be −(1/2)ln(1 + t^2 ) please am confuse in that integration ((1 − t)/(1 + t^2 ))dt why tan^(−1) (t) Thanks
$${Wow}\:{thanks} \\ $$$${why}\:{do}\:{we}\:{have}\:{tan}^{−\mathrm{1}} \:\left({t}\right) \\ $$$${i}\:{thought}\:\frac{\mathrm{1}\:−\:{t}}{\mathrm{1}\:+\:{t}^{\mathrm{2}} }\:{should}\:{be}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}\:+\:{t}^{\mathrm{2}} \right) \\ $$$${please}\:{am}\:{confuse}\:{in}\:{that}\:{integration} \\ $$$$\frac{\mathrm{1}\:−\:{t}}{\mathrm{1}\:+\:{t}^{\mathrm{2}} }{dt} \\ $$$${why}\:{tan}^{−\mathrm{1}} \left({t}\right)\:\:\:\:\:{Thanks} \\ $$
Commented by Tawakalitu. last updated on 09/Jul/16
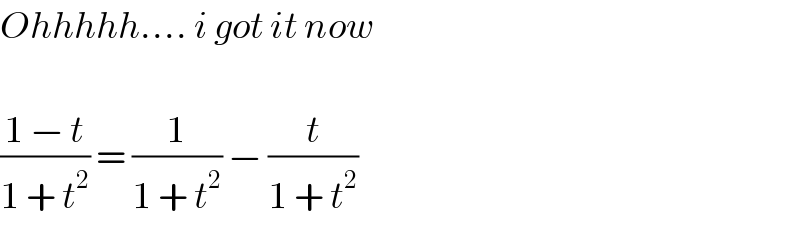
Ohhhhh.... i got it now ((1 − t)/(1 + t^2 )) = (1/(1 + t^2 )) − (t/(1 + t^2 ))
$${Ohhhhh}….\:{i}\:{got}\:{it}\:{now} \\ $$$$ \\ $$$$\frac{\mathrm{1}\:−\:{t}}{\mathrm{1}\:+\:{t}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{1}\:+\:{t}^{\mathrm{2}} }\:−\:\frac{{t}}{\mathrm{1}\:+\:{t}^{\mathrm{2}} } \\ $$
Commented by Tawakalitu. last updated on 09/Jul/16
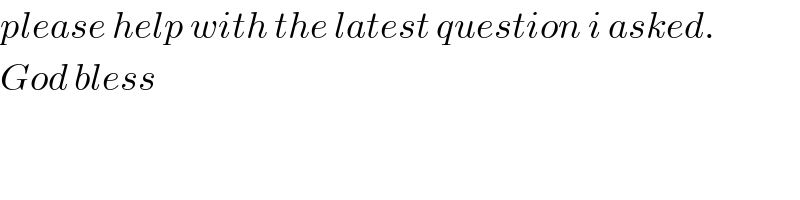
please help with the latest question i asked. God bless
$${please}\:{help}\:{with}\:{the}\:{latest}\:{question}\:{i}\:{asked}. \\ $$$${God}\:{bless} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *