Question Number 1096 by rpatle69@gmail.com last updated on 13/Jun/15
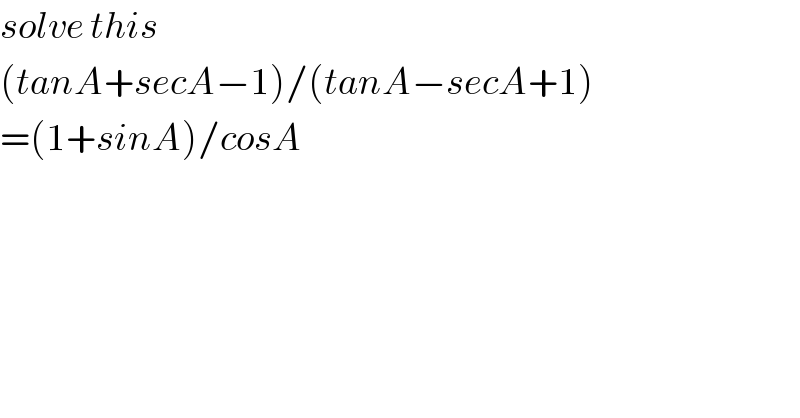
$${solve}\:{this} \\ $$$$\left({tanA}+{secA}−\mathrm{1}\right)/\left({tanA}−{secA}+\mathrm{1}\right) \\ $$$$=\left(\mathrm{1}+{sinA}\right)/{cosA} \\ $$$$ \\ $$
Answered by prakash jain last updated on 13/Jun/15

$$\frac{\mathrm{tan}\:{A}+\mathrm{sec}\:{A}−\mathrm{1}}{\mathrm{tan}\:{A}−\mathrm{sec}\:{A}+\mathrm{1}}=\mathrm{sec}\:{A}+\mathrm{tan}\:{A} \\ $$$$\mathrm{tan}\:{A}+\mathrm{sec}\:{A}−\mathrm{1}=\mathrm{sec}\:{A}\mathrm{tan}\:{A}−\mathrm{sec}^{\mathrm{2}} {A}+\mathrm{sec}\:{A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{tan}^{\mathrm{2}} {A}+\mathrm{tan}\:{A}−\mathrm{sec}\:{A}\mathrm{tan}\:{A} \\ $$$$\mathrm{tan}\:{A}+\mathrm{sec}\:{A}−\mathrm{1}=\mathrm{sec}\:{A}+\mathrm{tan}\:{A}−\left(\mathrm{sec}^{\mathrm{2}} {A}−\mathrm{tan}^{\mathrm{2}} {A}\right) \\ $$$$\mathrm{tan}\:{A}+\mathrm{sec}\:{A}−\mathrm{1}=\mathrm{sec}\:{A}+\mathrm{tan}\:{A}−\mathrm{1}\blacksquare \\ $$$$ \\ $$
