Question Number 133494 by Eric002 last updated on 22/Feb/21

$${solve}\:{without}\:{using}\:{l}'{hopital}\:{and}\:{series}\: \\ $$$$\underset{{x}\rightarrow\mathrm{8}} {\mathrm{lim}}\frac{{x}\:\sqrt[{\mathrm{3}}]{{x}}−\mathrm{16}}{{x}−\mathrm{8}} \\ $$
Answered by Olaf last updated on 22/Feb/21
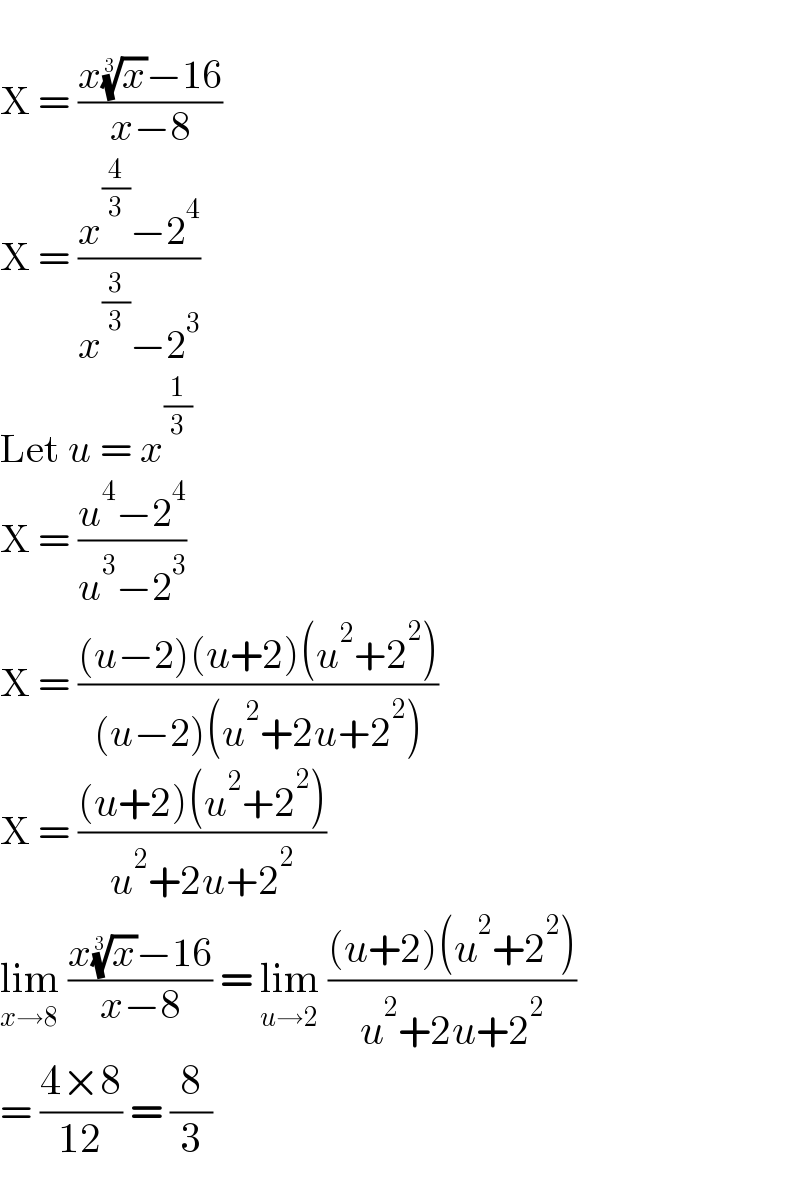
$$ \\ $$$$\mathrm{X}\:=\:\frac{{x}\sqrt[{\mathrm{3}}]{{x}}−\mathrm{16}}{{x}−\mathrm{8}} \\ $$$$\mathrm{X}\:=\:\frac{{x}^{\frac{\mathrm{4}}{\mathrm{3}}} −\mathrm{2}^{\mathrm{4}} }{{x}^{\frac{\mathrm{3}}{\mathrm{3}}} −\mathrm{2}^{\mathrm{3}} } \\ $$$$\mathrm{Let}\:{u}\:=\:{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\mathrm{X}\:=\:\frac{{u}^{\mathrm{4}} −\mathrm{2}^{\mathrm{4}} }{{u}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} } \\ $$$$\mathrm{X}\:=\:\frac{\left({u}−\mathrm{2}\right)\left({u}+\mathrm{2}\right)\left({u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right)}{\left({u}−\mathrm{2}\right)\left({u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{2}^{\mathrm{2}} \right)} \\ $$$$\mathrm{X}\:=\:\frac{\left({u}+\mathrm{2}\right)\left({u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{2}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{8}} {\mathrm{lim}}\:\frac{{x}\sqrt[{\mathrm{3}}]{{x}}−\mathrm{16}}{{x}−\mathrm{8}}\:=\:\underset{{u}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\left({u}+\mathrm{2}\right)\left({u}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{2}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{4}×\mathrm{8}}{\mathrm{12}}\:=\:\frac{\mathrm{8}}{\mathrm{3}} \\ $$
Commented by Eric002 last updated on 22/Feb/21

$${well}\:{done} \\ $$
Commented by otchereabdullai@gmail.com last updated on 14/Mar/21

$$\mathrm{nice}\:\mathrm{one} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Feb/21
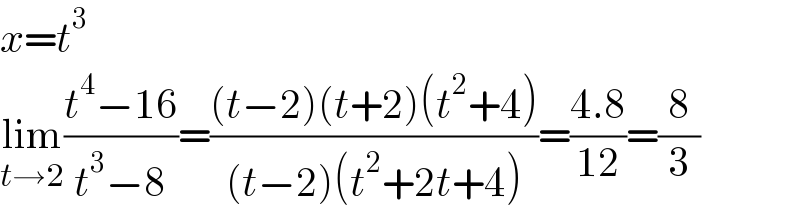
$${x}={t}^{\mathrm{3}} \\ $$$$\underset{{t}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{t}^{\mathrm{4}} −\mathrm{16}}{{t}^{\mathrm{3}} −\mathrm{8}}=\frac{\left({t}−\mathrm{2}\right)\left({t}+\mathrm{2}\right)\left({t}^{\mathrm{2}} +\mathrm{4}\right)}{\left({t}−\mathrm{2}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{4}\right)}=\frac{\mathrm{4}.\mathrm{8}}{\mathrm{12}}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$
Answered by malwan last updated on 22/Feb/21
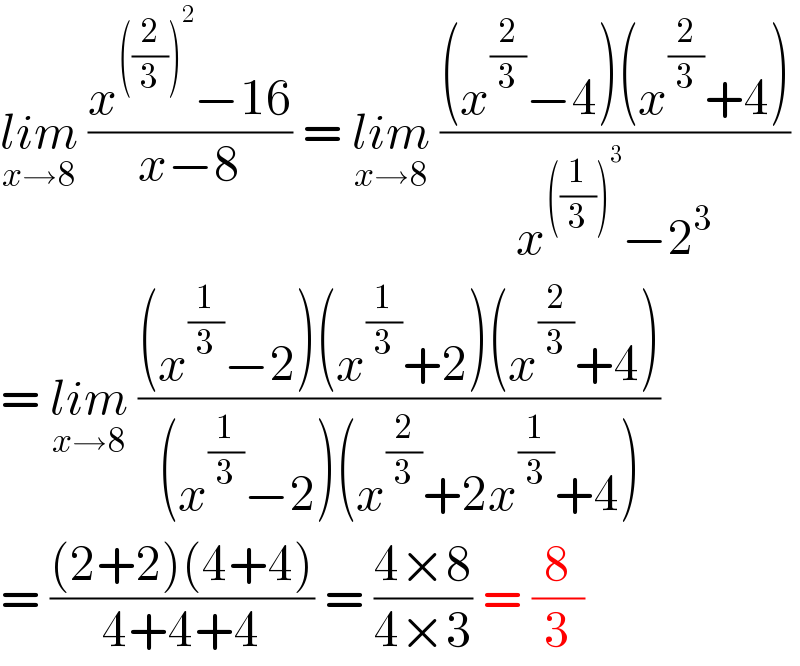
$$\underset{{x}\rightarrow\mathrm{8}} {{lim}}\:\frac{{x}^{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} } −\mathrm{16}}{{x}−\mathrm{8}}\:=\:\underset{{x}\rightarrow\mathrm{8}} {{lim}}\:\frac{\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{4}\right)\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{4}\right)}{{x}^{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} } −\mathrm{2}^{\mathrm{3}} } \\ $$$$=\:\underset{{x}\rightarrow\mathrm{8}} {{lim}}\:\frac{\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{2}\right)\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{2}\right)\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{4}\right)}{\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{2}\right)\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{2}{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{4}\right)} \\ $$$$=\:\frac{\left(\mathrm{2}+\mathrm{2}\right)\left(\mathrm{4}+\mathrm{4}\right)}{\mathrm{4}+\mathrm{4}+\mathrm{4}}\:=\:\frac{\mathrm{4}×\mathrm{8}}{\mathrm{4}×\mathrm{3}}\:=\:\frac{\mathrm{8}}{\mathrm{3}} \\ $$
