Menu Close

solve-x-2-7y-2-1-in-Z-

Tinku Tara 0 Comments
Pin




Question Number 739 by malwaan last updated on 08/Mar/15
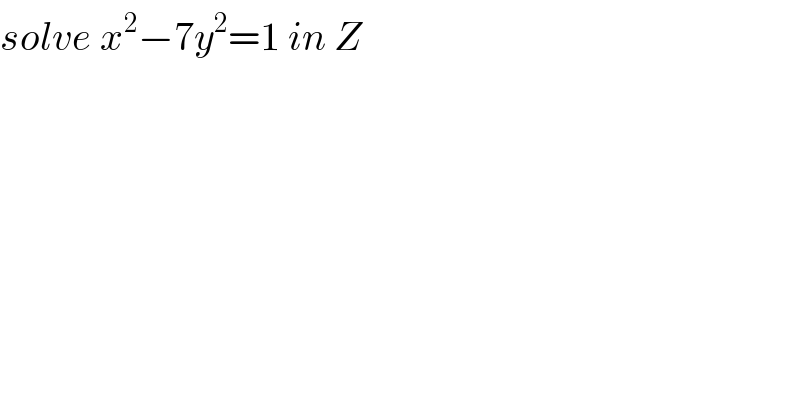
solve x^2 −7y^2 =1 in Z
$${solve}\:{x}^{\mathrm{2}} −\mathrm{7}{y}^{\mathrm{2}} =\mathrm{1}\:{in}\:{Z} \\ $$
Commented by 123456 last updated on 06/Mar/15
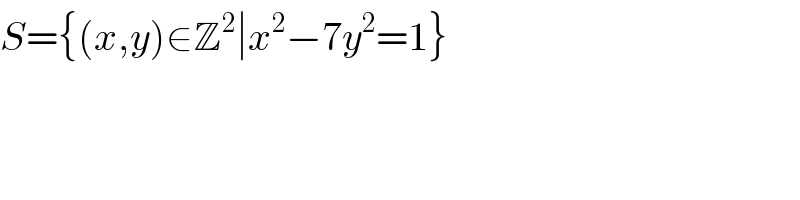
S={(x,y)∈Z^2 ∣x^2 −7y^2 =1}
$${S}=\left\{\left({x},{y}\right)\in\mathbb{Z}^{\mathrm{2}} \mid{x}^{\mathrm{2}} −\mathrm{7}{y}^{\mathrm{2}} =\mathrm{1}\right\} \\ $$
Commented by 123456 last updated on 06/Mar/15
(x,y)=(−1,0) (x,y)=(1,0) (x,y)=(8,3)
$$\left({x},{y}\right)=\left(−\mathrm{1},\mathrm{0}\right) \\ $$$$\left({x},{y}\right)=\left(\mathrm{1},\mathrm{0}\right) \\ $$$$\left({x},{y}\right)=\left(\mathrm{8},\mathrm{3}\right) \\ $$
Commented by 123456 last updated on 06/Mar/15
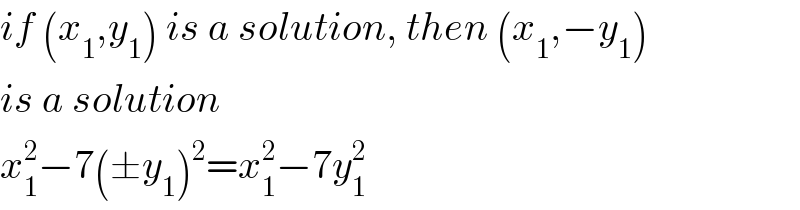
if (x_1 ,y_1 ) is a solution, then (x_1 ,−y_1 ) is a solution x_1 ^2 −7(±y_1 )^2 =x_1 ^2 −7y_1 ^2
$${if}\:\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)\:{is}\:{a}\:{solution},\:{then}\:\left({x}_{\mathrm{1}} ,−{y}_{\mathrm{1}} \right) \\ $$$${is}\:{a}\:{solution} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{7}\left(\pm{y}_{\mathrm{1}} \right)^{\mathrm{2}} ={x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{7}{y}_{\mathrm{1}} ^{\mathrm{2}} \\ $$
Commented by 123456 last updated on 06/Mar/15
(u^2 −7v^2 )(x^2 −7y^2 ) =u^2 x^2 −7u^2 y^2 −7v^2 x^2 +49v^2 y^2 =(ux)^2 +(7vy)^2 −7[(uy)^2 +(vx)^2 ] =(ux)^2 +(7vy)^2 −7[(uy)^2 +(vx)^2 ]+2(ux)(7vy)−2(ux)(vy) =(ux)^2 ±2(ux)(7vy)+(7vy)^2 −7[(uy)^2 ±2(uy)(vx)+(vx)^2 ] =(ux±7vy)^2 −7(uy±vx)^2 f:Z^4 →Z^2 f[(x_1 ,y_1 ),(x_2 ,y_2 )]=(x_1 x_2 +7y_1 y_2 ,x_1 y_2 +x_2 y_1 )
$$\left({u}^{\mathrm{2}} −\mathrm{7}{v}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\mathrm{7}{y}^{\mathrm{2}} \right) \\ $$$$={u}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{7}{u}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{7}{v}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{49}{v}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$=\left({ux}\right)^{\mathrm{2}} +\left(\mathrm{7}{vy}\right)^{\mathrm{2}} −\mathrm{7}\left[\left({uy}\right)^{\mathrm{2}} +\left({vx}\right)^{\mathrm{2}} \right] \\ $$$$=\left({ux}\right)^{\mathrm{2}} +\left(\mathrm{7}{vy}\right)^{\mathrm{2}} −\mathrm{7}\left[\left({uy}\right)^{\mathrm{2}} +\left({vx}\right)^{\mathrm{2}} \right]+\mathrm{2}\left({ux}\right)\left(\mathrm{7}{vy}\right)−\mathrm{2}\left({ux}\right)\left({vy}\right) \\ $$$$=\left({ux}\right)^{\mathrm{2}} \pm\mathrm{2}\left({ux}\right)\left(\mathrm{7}{vy}\right)+\left(\mathrm{7}{vy}\right)^{\mathrm{2}} −\mathrm{7}\left[\left({uy}\right)^{\mathrm{2}} \pm\mathrm{2}\left({uy}\right)\left({vx}\right)+\left({vx}\right)^{\mathrm{2}} \right] \\ $$$$=\left({ux}\pm\mathrm{7}{vy}\right)^{\mathrm{2}} −\mathrm{7}\left({uy}\pm{vx}\right)^{\mathrm{2}} \\ $$$${f}:\mathbb{Z}^{\mathrm{4}} \rightarrow\mathbb{Z}^{\mathrm{2}} \\ $$$${f}\left[\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right),\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right)\right]=\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +\mathrm{7}{y}_{\mathrm{1}} {y}_{\mathrm{2}} ,{x}_{\mathrm{1}} {y}_{\mathrm{2}} +{x}_{\mathrm{2}} {y}_{\mathrm{1}} \right) \\ $$
Answered by prakash jain last updated on 06/Mar/15
7y^2 =x^2 −1=(x+1)(x−1) 7 divides (x+1)(x−1)⇒x=7k+1 or 7k−1 Case I: x=7k+1 7y^2 =7k(7k+2)⇒y^2 =k(7k+2) k(7k+2) is perfect square so k is a factor of 7k+2. ((7k+2)/k)=7+(2/k) Only possible values for k are 0, ±1, ±2 k=0, k(7k+2)=0=0^2 ⇒y=0, x=7k+1=1 k=1, k(7k+2)=9=3^2 ⇒y=±3, x=7k+1=8 k=−1, k(7k+2)=5 (not a perfect square) k=2, k(7k+2)=32 (not a perfect square) k=−2, k(7k+2)=24 (not a perfect square) Case II: x=7k−1 y^2 =k(7k−2) As above k=0, ±1,±2 k=0, k(7k−2)=0=0^2 ⇒y=0, x=7k−1=−1 k=1, k(7k−2)=5 (not a perfect square) k=−1, k(7k−2)=9=3^2 ⇒y=±3, x=7k−1=−8 k=2, k(7k−2)=24 (not a perfect square) k=−2, k(7k−2)=32 (not a perfect square) So the only solution x^2 −7y^2 =1 are x=−1,y =0 x=1, y=0 x=8, y=±3 x=−8, y=±3
$$\mathrm{7}{y}^{\mathrm{2}} ={x}^{\mathrm{2}} −\mathrm{1}=\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right) \\ $$$$\mathrm{7}\:\mathrm{divides}\:\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)\Rightarrow{x}=\mathrm{7}{k}+\mathrm{1}\:\mathrm{or}\:\mathrm{7}{k}−\mathrm{1} \\ $$$$\mathrm{Case}\:\mathrm{I}:\:{x}=\mathrm{7}{k}+\mathrm{1} \\ $$$$\mathrm{7}{y}^{\mathrm{2}} =\mathrm{7}{k}\left(\mathrm{7}{k}+\mathrm{2}\right)\Rightarrow{y}^{\mathrm{2}} ={k}\left(\mathrm{7}{k}+\mathrm{2}\right) \\ $$$${k}\left(\mathrm{7}{k}+\mathrm{2}\right)\:\mathrm{is}\:\mathrm{perfect}\:\mathrm{square}\:\mathrm{so}\:{k}\:\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of} \\ $$$$\mathrm{7}{k}+\mathrm{2}. \\ $$$$\frac{\mathrm{7}{k}+\mathrm{2}}{{k}}=\mathrm{7}+\frac{\mathrm{2}}{{k}} \\ $$$$\mathrm{Only}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{for}\:{k}\:\mathrm{are}\:\mathrm{0},\:\pm\mathrm{1},\:\pm\mathrm{2} \\ $$$${k}=\mathrm{0},\:{k}\left(\mathrm{7}{k}+\mathrm{2}\right)=\mathrm{0}=\mathrm{0}^{\mathrm{2}} \Rightarrow{y}=\mathrm{0},\:{x}=\mathrm{7}{k}+\mathrm{1}=\mathrm{1} \\ $$$${k}=\mathrm{1},\:{k}\left(\mathrm{7}{k}+\mathrm{2}\right)=\mathrm{9}=\mathrm{3}^{\mathrm{2}} \Rightarrow{y}=\pm\mathrm{3},\:{x}=\mathrm{7}{k}+\mathrm{1}=\mathrm{8} \\ $$$${k}=−\mathrm{1},\:{k}\left(\mathrm{7}{k}+\mathrm{2}\right)=\mathrm{5}\:\left(\mathrm{not}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\right) \\ $$$${k}=\mathrm{2},\:\mathrm{k}\left(\mathrm{7}{k}+\mathrm{2}\right)=\mathrm{32}\:\left(\mathrm{not}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\right) \\ $$$${k}=−\mathrm{2},\:\mathrm{k}\left(\mathrm{7}{k}+\mathrm{2}\right)=\mathrm{24}\:\left(\mathrm{not}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\right) \\ $$$$\mathrm{Case}\:\mathrm{II}:\:{x}=\mathrm{7}{k}−\mathrm{1} \\ $$$${y}^{\mathrm{2}} ={k}\left(\mathrm{7}{k}−\mathrm{2}\right) \\ $$$$\mathrm{As}\:\mathrm{above}\:{k}=\mathrm{0},\:\pm\mathrm{1},\pm\mathrm{2} \\ $$$${k}=\mathrm{0},\:{k}\left(\mathrm{7}{k}−\mathrm{2}\right)=\mathrm{0}=\mathrm{0}^{\mathrm{2}} \Rightarrow{y}=\mathrm{0},\:{x}=\mathrm{7}{k}−\mathrm{1}=−\mathrm{1} \\ $$$${k}=\mathrm{1},\:{k}\left(\mathrm{7}{k}−\mathrm{2}\right)=\mathrm{5}\:\left(\mathrm{not}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\right) \\ $$$${k}=−\mathrm{1},\:{k}\left(\mathrm{7}{k}−\mathrm{2}\right)=\mathrm{9}=\mathrm{3}^{\mathrm{2}} \Rightarrow{y}=\pm\mathrm{3},\:{x}=\mathrm{7}{k}−\mathrm{1}=−\mathrm{8} \\ $$$${k}=\mathrm{2},\:{k}\left(\mathrm{7}{k}−\mathrm{2}\right)=\mathrm{24}\:\left(\mathrm{not}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\right) \\ $$$${k}=−\mathrm{2},\:{k}\left(\mathrm{7}{k}−\mathrm{2}\right)=\mathrm{32}\:\left(\mathrm{not}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{square}\right) \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solution}\:{x}^{\mathrm{2}} −\mathrm{7}{y}^{\mathrm{2}} =\mathrm{1}\:\mathrm{are} \\ $$$${x}=−\mathrm{1},{y}\:=\mathrm{0} \\ $$$${x}=\mathrm{1},\:{y}=\mathrm{0} \\ $$$${x}=\mathrm{8},\:{y}=\pm\mathrm{3} \\ $$$${x}=−\mathrm{8},\:{y}=\pm\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *