Question Number 8515 by Basant007 last updated on 14/Oct/16
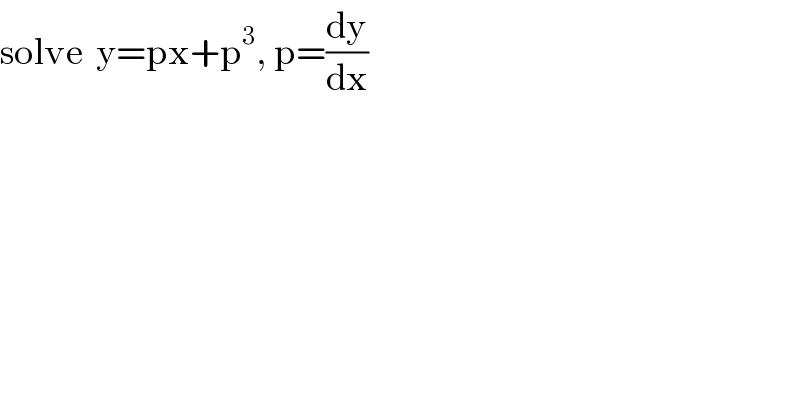
$$\mathrm{solve}\:\:\mathrm{y}=\mathrm{px}+\mathrm{p}^{\mathrm{3}} ,\:\mathrm{p}=\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$
Commented by prakash jain last updated on 14/Oct/16

$$\mathrm{differentiaing} \\ $$$${p}={p}+{x}\frac{{dp}}{{dx}}+\mathrm{3}{p}^{\mathrm{2}} \frac{{dp}}{{dx}} \\ $$$$\mathrm{3}{p}^{\mathrm{2}} \frac{{dp}}{{dx}}+{x}\frac{{dp}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dp}}{{dx}}\left(\mathrm{3}{p}^{\mathrm{2}} +{x}\right)=\mathrm{0} \\ $$$${case}\:{i} \\ $$$$\frac{{dp}}{{dx}}=\mathrm{0} \\ $$$${p}={c} \\ $$$$\frac{{dy}}{{dx}}={c} \\ $$$${y}={cx}+{d} \\ $$$${substituting}\:{in}\:{original}\:{equation} \\ $$$${cx}+{d}={cx}+{c}^{\mathrm{3}} \\ $$$${y}={cx}+{c}^{\mathrm{3}} \\ $$$${case}\:\mathrm{2} \\ $$$$\mathrm{3}{p}^{\mathrm{2}} =−{x} \\ $$$${p}=\frac{{dy}}{{dx}}=\frac{\pm{i}\sqrt{{x}}}{\:\sqrt{\mathrm{3}}} \\ $$$${p}\:\mathrm{is}\:\mathrm{not}\:\mathrm{real} \\ $$
Commented by prakash jain last updated on 14/Oct/16

$${y}={ax}+{a}^{\mathrm{3}} \\ $$
Commented by prakash jain last updated on 14/Oct/16
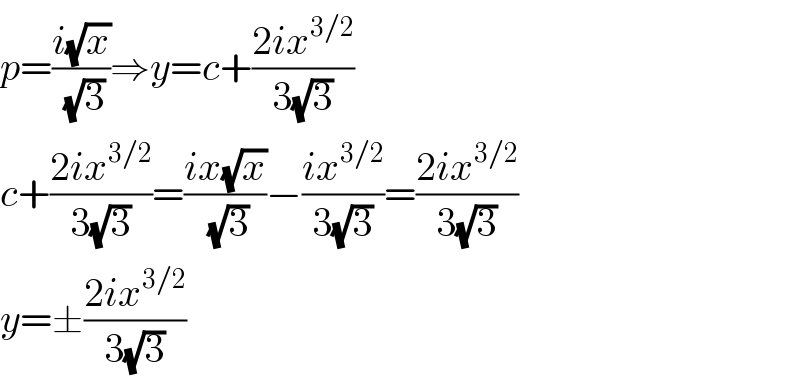
$${p}=\frac{{i}\sqrt{{x}}}{\:\sqrt{\mathrm{3}}}\Rightarrow{y}={c}+\frac{\mathrm{2}{ix}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${c}+\frac{\mathrm{2}{ix}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}=\frac{{ix}\sqrt{{x}}}{\:\sqrt{\mathrm{3}}}−\frac{{ix}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}=\frac{\mathrm{2}{ix}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${y}=\pm\frac{\mathrm{2}{ix}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
