Menu Close

solve-y-y-y-e-x-e-2x-y-0-y-0-1-y-0-y-0-0-

Tinku Tara
Pin




Question Number 236 by 123456 last updated on 25/Jan/15
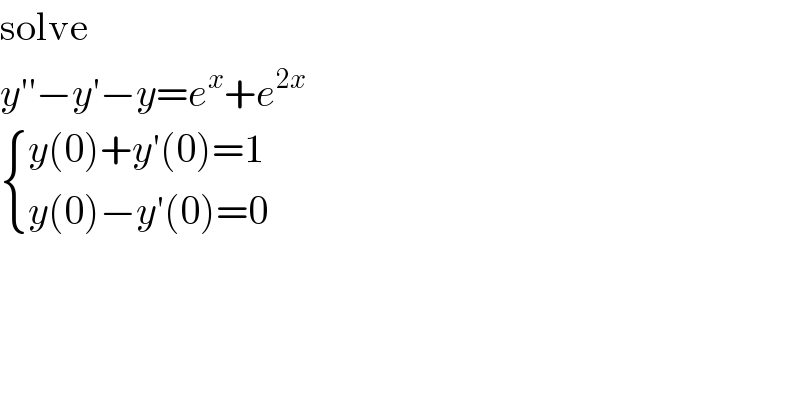
solve y′′−y′−y=e^x +e^(2x) { ((y(0)+y′(0)=1)),((y(0)−y′(0)=0)) :}
$$\mathrm{solve} \\ $$$${y}''−{y}'−{y}={e}^{{x}} +{e}^{\mathrm{2}{x}} \\ $$$$\begin{cases}{{y}\left(\mathrm{0}\right)+{y}'\left(\mathrm{0}\right)=\mathrm{1}}\\{{y}\left(\mathrm{0}\right)−{y}'\left(\mathrm{0}\right)=\mathrm{0}}\end{cases} \\ $$
Answered by prakash jain last updated on 17/Dec/14
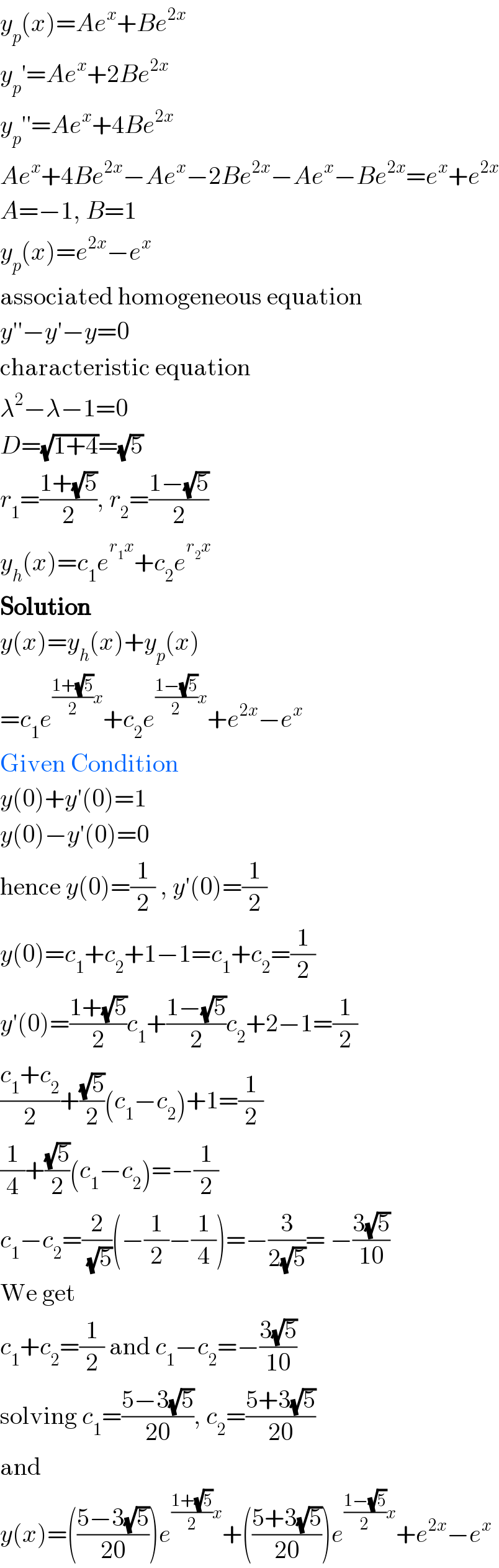
y_p (x)=Ae^x +Be^(2x) y_p ′=Ae^x +2Be^(2x) y_p ′′=Ae^x +4Be^(2x) Ae^x +4Be^(2x) −Ae^x −2Be^(2x) −Ae^x −Be^(2x) =e^x +e^(2x) A=−1, B=1 y_p (x)=e^(2x) −e^x associated homogeneous equation y′′−y′−y=0 characteristic equation λ^2 −λ−1=0 D=(√(1+4))=(√5) r_1 =((1+(√5))/2), r_2 =((1−(√5))/2) y_h (x)=c_1 e^(r_1 x) +c_2 e^(r_2 x) Solution y(x)=y_h (x)+y_p (x) =c_1 e^(((1+(√5))/2)x) +c_2 e^(((1−(√5))/2)x) +e^(2x) −e^x Given Condition y(0)+y′(0)=1 y(0)−y′(0)=0 hence y(0)=(1/2) , y′(0)=(1/2) y(0)=c_1 +c_2 +1−1=c_1 +c_2 =(1/2) y′(0)=((1+(√5))/2)c_1 +((1−(√5))/2)c_2 +2−1=(1/2) ((c_1 +c_2 )/2)+((√5)/2)(c_1 −c_2 )+1=(1/2) (1/4)+((√5)/2)(c_1 −c_2 )=−(1/2) c_1 −c_2 =(2/( (√5)))(−(1/2)−(1/4))=−(3/(2(√5)))= −((3(√5))/(10)) We get c_1 +c_2 =(1/2) and c_1 −c_2 =−((3(√5))/(10)) solving c_1 =((5−3(√5))/(20)), c_2 =((5+3(√5))/(20)) and y(x)=(((5−3(√5))/(20)))e^(((1+(√5))/2)x) +(((5+3(√5))/(20)))e^(((1−(√5))/2)x) +e^(2x) −e^x
$${y}_{{p}} \left({x}\right)={Ae}^{{x}} +{Be}^{\mathrm{2}{x}} \\ $$$${y}_{{p}} '={Ae}^{{x}} +\mathrm{2}{Be}^{\mathrm{2}{x}} \\ $$$${y}_{{p}} ''={Ae}^{{x}} +\mathrm{4}{Be}^{\mathrm{2}{x}} \\ $$$${Ae}^{{x}} +\mathrm{4}{Be}^{\mathrm{2}{x}} −{Ae}^{{x}} −\mathrm{2}{Be}^{\mathrm{2}{x}} −{Ae}^{{x}} −{Be}^{\mathrm{2}{x}} ={e}^{{x}} +{e}^{\mathrm{2}{x}} \\ $$$${A}=−\mathrm{1},\:{B}=\mathrm{1} \\ $$$${y}_{{p}} \left({x}\right)={e}^{\mathrm{2}{x}} −{e}^{{x}} \\ $$$$\mathrm{associated}\:\mathrm{homogeneous}\:\mathrm{equation} \\ $$$${y}''−{y}'−{y}=\mathrm{0} \\ $$$$\mathrm{characteristic}\:\mathrm{equation} \\ $$$$\lambda^{\mathrm{2}} −\lambda−\mathrm{1}=\mathrm{0} \\ $$$${D}=\sqrt{\mathrm{1}+\mathrm{4}}=\sqrt{\mathrm{5}} \\ $$$${r}_{\mathrm{1}} =\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\:{r}_{\mathrm{2}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${y}_{{h}} \left({x}\right)={c}_{\mathrm{1}} {e}^{{r}_{\mathrm{1}} {x}} +{c}_{\mathrm{2}} {e}^{{r}_{\mathrm{2}} {x}} \\ $$$$\boldsymbol{\mathrm{Solution}} \\ $$$${y}\left({x}\right)={y}_{{h}} \left({x}\right)+{y}_{{p}} \left({x}\right) \\ $$$$={c}_{\mathrm{1}} {e}^{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}} +{c}_{\mathrm{2}} {e}^{\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}} +{e}^{\mathrm{2}{x}} −{e}^{{x}} \\ $$$$\mathrm{Given}\:\mathrm{Condition} \\ $$$${y}\left(\mathrm{0}\right)+{y}'\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${y}\left(\mathrm{0}\right)−{y}'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{hence}\:{y}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:,\:{y}'\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}\left(\mathrm{0}\right)={c}_{\mathrm{1}} +{c}_{\mathrm{2}} +\mathrm{1}−\mathrm{1}={c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}'\left(\mathrm{0}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{c}_{\mathrm{1}} +\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{c}_{\mathrm{2}} +\mathrm{2}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{c}_{\mathrm{1}} +{c}_{\mathrm{2}} }{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\left({c}_{\mathrm{1}} −{c}_{\mathrm{2}} \right)+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\left({c}_{\mathrm{1}} −{c}_{\mathrm{2}} \right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${c}_{\mathrm{1}} −{c}_{\mathrm{2}} =\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right)=−\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{5}}}=\:−\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$$\mathrm{We}\:\mathrm{get}\: \\ $$$${c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:{c}_{\mathrm{1}} −{c}_{\mathrm{2}} =−\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$$\mathrm{solving}\:{c}_{\mathrm{1}} =\frac{\mathrm{5}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{20}},\:{c}_{\mathrm{2}} =\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{20}} \\ $$$$\mathrm{and} \\ $$$${y}\left({x}\right)=\left(\frac{\mathrm{5}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{20}}\right){e}^{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}} +\left(\frac{\mathrm{5}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{20}}\right){e}^{\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}} +{e}^{\mathrm{2}{x}} −{e}^{{x}} \\ $$

Pin