Menu Close

solving-for-B-U-b-U-s-2-n-1-g-sin-B-n-H-n-1-

Tinku Tara 0 Comments
Pin




Question Number 8695 by vuckintv last updated on 22/Oct/16
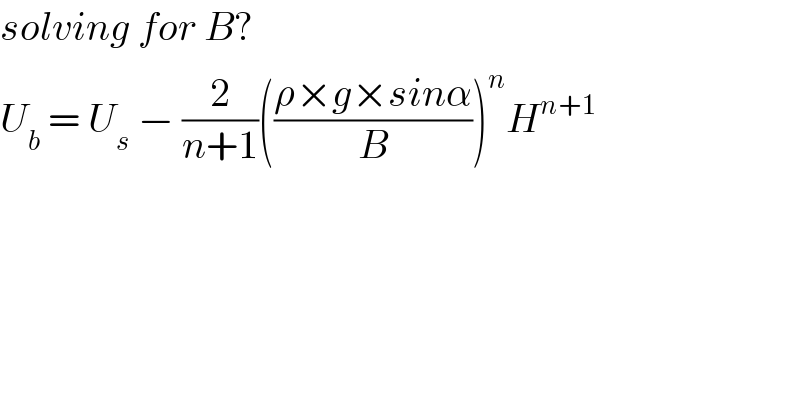
solving for B? U_b = U_s − (2/(n+1))(((ρ×g×sinα)/B))^n H^(n+1)
solvingforB?Ub=Us−2n+1(ρ×g×sinαB)nHn+1
Answered by FilupSmith last updated on 22/Oct/16
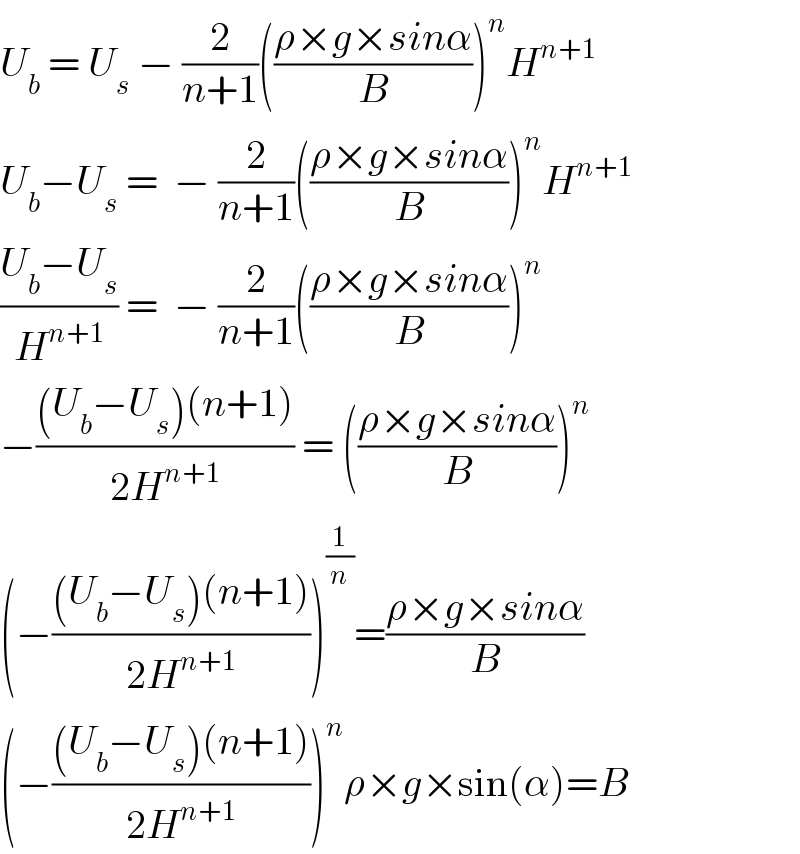
U_b = U_s − (2/(n+1))(((ρ×g×sinα)/B))^n H^(n+1) U_b −U_s = − (2/(n+1))(((ρ×g×sinα)/B))^n H^(n+1) ((U_b −U_s )/H^(n+1) ) = − (2/(n+1))(((ρ×g×sinα)/B))^n −(((U_b −U_s )(n+1))/(2H^(n+1) )) = (((ρ×g×sinα)/B))^n (−(((U_b −U_s )(n+1))/(2H^(n+1) )))^(1/n) =((ρ×g×sinα)/B) (−(((U_b −U_s )(n+1))/(2H^(n+1) )))^n ρ×g×sin(α)=B
Ub=Us−2n+1(ρ×g×sinαB)nHn+1Ub−Us=−2n+1(ρ×g×sinαB)nHn+1Ub−UsHn+1=−2n+1(ρ×g×sinαB)n−(Ub−Us)(n+1)2Hn+1=(ρ×g×sinαB)n(−(Ub−Us)(n+1)2Hn+1)1n=ρ×g×sinαB(−(Ub−Us)(n+1)2Hn+1)nρ×g×sin(α)=B
Commented by Rasheed Soomro last updated on 22/Oct/16
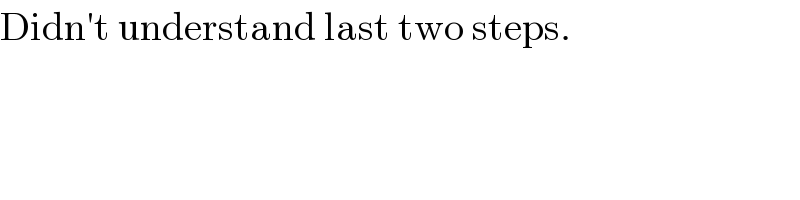
Didn′t understand last two steps.
Didn′tunderstandlasttwosteps.
Answered by Rasheed Soomro last updated on 22/Oct/16
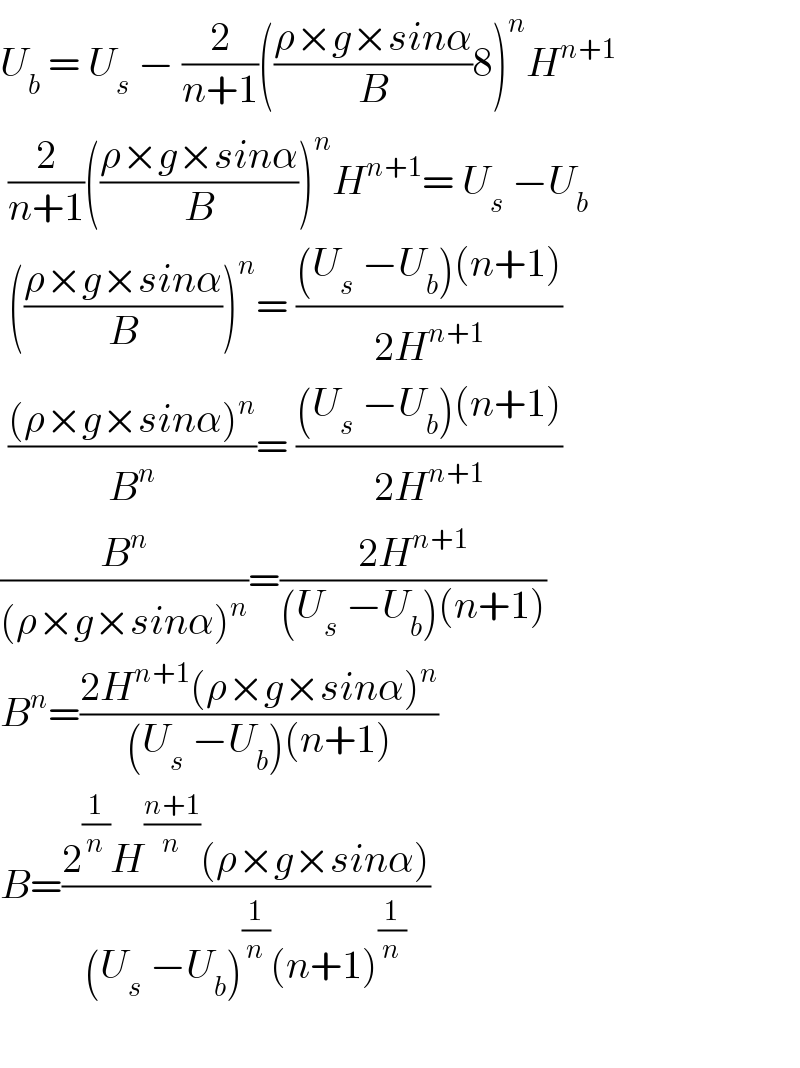
U_b = U_s − (2/(n+1))(((ρ×g×sinα)/B)8)^n H^(n+1) (2/(n+1))(((ρ×g×sinα)/B))^n H^(n+1) = U_s −U_b (((ρ×g×sinα)/B))^n = (((U_s −U_b )(n+1))/(2H^(n+1) )) (((ρ×g×sinα)^n )/B^n )= (((U_s −U_b )(n+1))/(2H^(n+1) )) (B^n /((ρ×g×sinα)^n ))=((2H^(n+1) )/((U_s −U_b )(n+1))) B^n =((2H^(n+1) (ρ×g×sinα)^n )/((U_s −U_b )(n+1))) B=((2^(1/n) H^((n+1)/n) (ρ×g×sinα))/((U_s −U_b )^(1/n) (n+1)^(1/n) ))
Ub=Us−2n+1(ρ×g×sinαB8)nHn+12n+1(ρ×g×sinαB)nHn+1=Us−Ub(ρ×g×sinαB)n=(Us−Ub)(n+1)2Hn+1(ρ×g×sinα)nBn=(Us−Ub)(n+1)2Hn+1Bn(ρ×g×sinα)n=2Hn+1(Us−Ub)(n+1)Bn=2Hn+1(ρ×g×sinα)n(Us−Ub)(n+1)B=21nHn+1n(ρ×g×sinα)(Us−Ub)1n(n+1)1n
Commented by vuckintv last updated on 22/Oct/16
Thank you
Thankyou

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *