Question Number 70135 by petrochengula last updated on 01/Oct/19

$${sophie}−{Germain}\:{identity} \\ $$$${a}^{\mathrm{4}} +\mathrm{4}{b}^{\mathrm{4}} =\left(\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left(\left({a}−{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$
Commented by mathmax by abdo last updated on 02/Oct/19
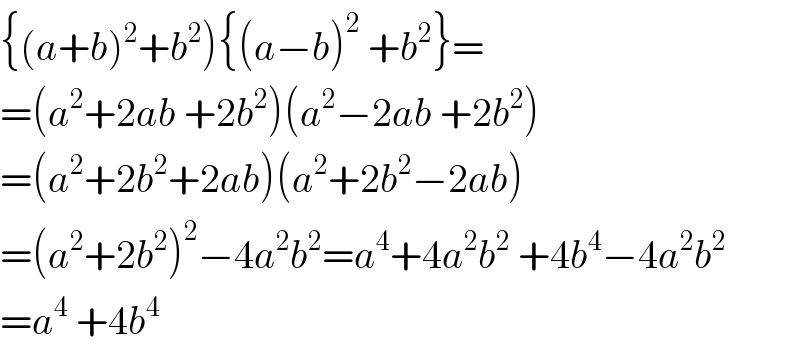
$$\left\{\left({a}+{b}\right)^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left\{\left({a}−{b}\right)^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right\}= \\ $$$$=\left({a}^{\mathrm{2}} +\mathrm{2}{ab}\:+\mathrm{2}{b}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} −\mathrm{2}{ab}\:+\mathrm{2}{b}^{\mathrm{2}} \right) \\ $$$$=\left({a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{ab}\right)\left({a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{ab}\right) \\ $$$$=\left({a}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} ={a}^{\mathrm{4}} +\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \:+\mathrm{4}{b}^{\mathrm{4}} −\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$={a}^{\mathrm{4}} \:+\mathrm{4}{b}^{\mathrm{4}} \\ $$
