Menu Close

sove-the-de-1-2-x-y-x-x-1-y-xsin-2x-

Tinku Tara 0 Comments
Pin




Question Number 66789 by mathmax by abdo last updated on 19/Aug/19
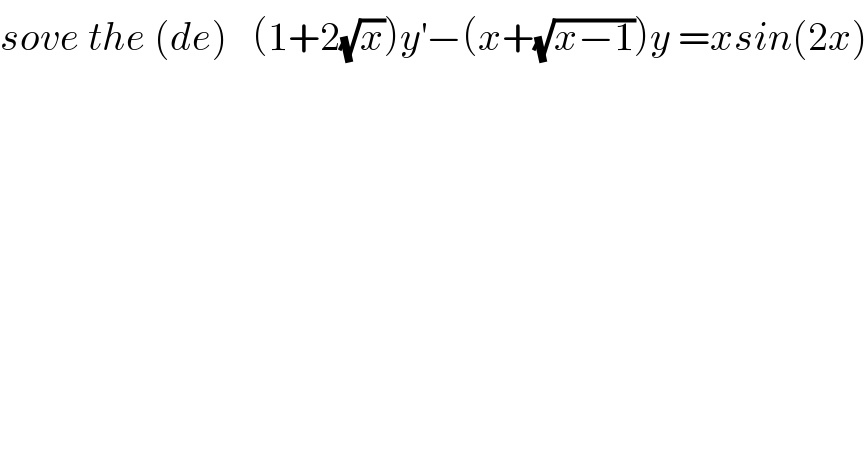
sove the (de) (1+2(√x))y^′ −(x+(√(x−1)))y =xsin(2x)
$${sove}\:{the}\:\left({de}\right)\:\:\:\left(\mathrm{1}+\mathrm{2}\sqrt{{x}}\right){y}^{'} −\left({x}+\sqrt{{x}−\mathrm{1}}\right){y}\:={xsin}\left(\mathrm{2}{x}\right) \\ $$
Commented by mathmax by abdo last updated on 20/Aug/19
(he) →(1+2(√x))y^′ −(x+(√(x−1)))y =0 ⇒(1+2(√x))y^′ =(x+(√(x−1)))y ⇒ (y^′ /y) =((x+(√(x−1)))/(1+2(√x))) ⇒ln∣y∣ =∫ ((x+(√(x−1)))/(1+2(√x)))dx =_(x=t^2 ) ∫ ((t^2 +(√(t^2 −1)))/(1+2t))(2t)dt =2 ∫ ((t^3 +t(√(t^2 −1)))/(2t+1))dt =2 ∫ (t^3 /(2t+1))dt +∫ (((2t+1−1)(√(t^2 −1)))/(2t+1))dt =2 ∫ (t^3 /(2t+1))dt +∫ (√(t^2 −1))dt−∫ ((√(t^2 −1))/(2t +1))dt we have ∫ ((2t^3 )/(2t+1))dt =(1/4)∫ ((8t^3 +1−1)/(2t+1))dt =(1/4)∫ (((2t+1)((2t)^2 −2t+1)−1)/(2t+1))dt =(1/4)∫ (4t^2 −2t+1)dt −(1/4)∫ (dt/(2t+1))=∫(t^2 −(t/2) +(1/4))dt−(1/8)ln∣2t+1∣ =(t^3 /3)−(t^2 /4) +(t/4)−(1/8)ln∣2t+1∣ +c_1 =((((√x))^3 )/3)−(x/4)+((√x)/4)−(1/8)ln∣2(√x)+1∣+c_1 ∫ (√(t^2 −1))dt =_(t=chu) ∫shushu du =∫((ch(2u)−1)/2)du =(1/4)sh(2u)−(u/2) =(1/2)shuchu−(u/2)=(t/2)(√(t^2 −1))−((ln(t+(√(t^2 −1))))/2) =((√x)/2)(√(x−1))−(1/2)ln((√x)+(√(x−1))) +c_2 ∫((√(t^2 −1))/(2t+1)) dt =_(t=chu) ∫ ((shu)/(2chu+1))shu du =∫ ((sh^2 u)/(2chu+1))du =(1/2)∫ ((ch(2u)−1)/(2chu+1))du =(1/2)∫ (((e^(2u +e^(−2u) ) /2)−1)/(e^u +e^(−u) +1))du =(1/4)∫ ((e^(2u) −e^(−2u) −2)/(e^u +e^(−u) +1))du =_(e^u =α) (1/4)∫ ((α^2 −α^(−2) −2)/(α+α^(−1) +1)) (dα/α) =(1/4)∫ ((α^2 −α^(−2) −2)/(α^2 +1+α))dα =(1/4)∫ ((α^4 −1+2α^2 )/(α^4 +α^3 +α^2 ))dα....becontinued...
$$\left({he}\right)\:\rightarrow\left(\mathrm{1}+\mathrm{2}\sqrt{{x}}\right){y}^{'} −\left({x}+\sqrt{{x}−\mathrm{1}}\right){y}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{1}+\mathrm{2}\sqrt{{x}}\right){y}^{'} =\left({x}+\sqrt{{x}−\mathrm{1}}\right){y}\:\Rightarrow \\ $$$$\frac{{y}^{'} }{{y}}\:=\frac{{x}+\sqrt{{x}−\mathrm{1}}}{\mathrm{1}+\mathrm{2}\sqrt{{x}}}\:\Rightarrow{ln}\mid{y}\mid\:=\int\:\frac{{x}+\sqrt{{x}−\mathrm{1}}}{\mathrm{1}+\mathrm{2}\sqrt{{x}}}{dx}\:=_{{x}={t}^{\mathrm{2}} } \:\:\:\int\:\:\frac{{t}^{\mathrm{2}} \:+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{1}+\mathrm{2}{t}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{3}} \:+{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}{t}+\mathrm{1}}{dt}\:=\mathrm{2}\:\int\:\frac{{t}^{\mathrm{3}} }{\mathrm{2}{t}+\mathrm{1}}{dt}\:+\int\:\:\frac{\left(\mathrm{2}{t}+\mathrm{1}−\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}{t}+\mathrm{1}}{dt} \\ $$$$=\mathrm{2}\:\int\:\frac{{t}^{\mathrm{3}} }{\mathrm{2}{t}+\mathrm{1}}{dt}\:+\int\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}{dt}−\int\:\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}{t}\:+\mathrm{1}}{dt}\:\:{we}\:{have} \\ $$$$\int\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} }{\mathrm{2}{t}+\mathrm{1}}{dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\:\frac{\mathrm{8}{t}^{\mathrm{3}} +\mathrm{1}−\mathrm{1}}{\mathrm{2}{t}+\mathrm{1}}{dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{\left(\mathrm{2}{t}+\mathrm{1}\right)\left(\left(\mathrm{2}{t}\right)^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)−\mathrm{1}}{\mathrm{2}{t}+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right){dt}\:−\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{{dt}}{\mathrm{2}{t}+\mathrm{1}}=\int\left({t}^{\mathrm{2}} −\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\right){dt}−\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid\mathrm{2}{t}+\mathrm{1}\mid \\ $$$$=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\:+\frac{{t}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid\mathrm{2}{t}+\mathrm{1}\mid\:+{c}_{\mathrm{1}} \:=\frac{\left(\sqrt{{x}}\right)^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}}{\mathrm{4}}+\frac{\sqrt{{x}}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid\mathrm{2}\sqrt{{x}}+\mathrm{1}\mid+{c}_{\mathrm{1}} \\ $$$$\int\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=_{{t}={chu}} \:\:\:\int{shushu}\:{du}\:=\int\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{u}\right)−\frac{{u}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}{shuchu}−\frac{{u}}{\mathrm{2}}=\frac{{t}}{\mathrm{2}}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}−\frac{{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)}{\mathrm{2}} \\ $$$$=\frac{\sqrt{{x}}}{\mathrm{2}}\sqrt{{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\sqrt{{x}}+\sqrt{{x}−\mathrm{1}}\right)\:+{c}_{\mathrm{2}} \\ $$$$\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}{t}+\mathrm{1}}\:{dt}\:=_{{t}={chu}} \:\:\:\:\int\:\frac{{shu}}{\mathrm{2}{chu}+\mathrm{1}}{shu}\:{du}\:=\int\:\:\frac{{sh}^{\mathrm{2}} {u}}{\mathrm{2}{chu}+\mathrm{1}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}{chu}+\mathrm{1}}{du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\frac{{e}^{\mathrm{2}{u}\:+{e}^{−\mathrm{2}{u}} } }{\mathrm{2}}−\mathrm{1}}{{e}^{{u}} \:+{e}^{−{u}} \:+\mathrm{1}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{{e}^{\mathrm{2}{u}} −{e}^{−\mathrm{2}{u}} −\mathrm{2}}{{e}^{{u}} \:+{e}^{−{u}} \:+\mathrm{1}}{du}\:=_{{e}^{{u}} \:=\alpha} \:\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\alpha^{\mathrm{2}} −\alpha^{−\mathrm{2}} −\mathrm{2}}{\alpha+\alpha^{−\mathrm{1}} +\mathrm{1}}\:\frac{{d}\alpha}{\alpha} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\:\frac{\alpha^{\mathrm{2}} −\alpha^{−\mathrm{2}} −\mathrm{2}}{\alpha^{\mathrm{2}} \:+\mathrm{1}+\alpha}{d}\alpha\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{\alpha^{\mathrm{4}} −\mathrm{1}+\mathrm{2}\alpha^{\mathrm{2}} }{\alpha^{\mathrm{4}} +\alpha^{\mathrm{3}} \:+\alpha^{\mathrm{2}} }{d}\alpha….{becontinued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *