Question Number 138037 by greg_ed last updated on 09/Apr/21
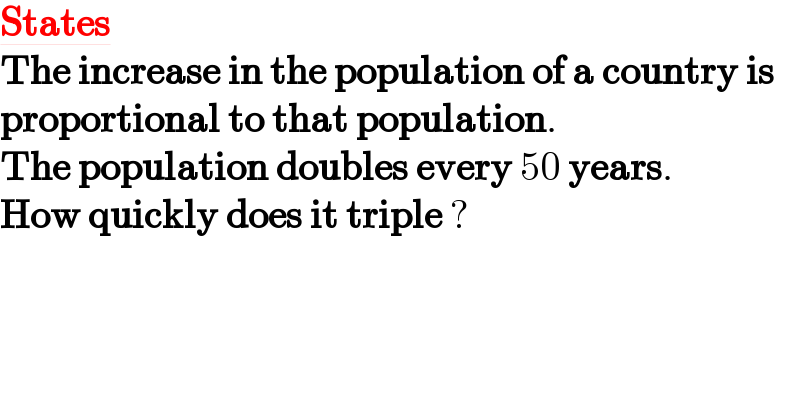
$$\underline{\boldsymbol{\mathrm{States}}} \\ $$$$\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{increase}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{population}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{country}}\:\boldsymbol{\mathrm{is}} \\ $$$$\boldsymbol{\mathrm{proportional}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{population}}. \\ $$$$\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{population}}\:\boldsymbol{\mathrm{doubles}}\:\boldsymbol{\mathrm{every}}\:\mathrm{50}\:\boldsymbol{\mathrm{years}}. \\ $$$$\boldsymbol{\mathrm{How}}\:\boldsymbol{\mathrm{quickly}}\:\boldsymbol{\mathrm{does}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{triple}}\:? \\ $$
Answered by MJS_new last updated on 09/Apr/21

$$\mathrm{2}^{\frac{{y}}{\mathrm{50}}} =\mathrm{3} \\ $$$$\frac{{y}}{\mathrm{50}}\mathrm{ln}\:\mathrm{2}\:=\mathrm{ln}\:\mathrm{3} \\ $$$${y}=\mathrm{50}\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}\approx\mathrm{79}.\mathrm{25} \\ $$
Commented by greg_ed last updated on 09/Apr/21

$$\boldsymbol{\mathrm{thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{very}}\:\boldsymbol{\mathrm{much}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{promptness}},\: \\ $$$$\boldsymbol{\mathrm{dear}}\:\boldsymbol{\mathrm{friend}}\:! \\ $$
Answered by mr W last updated on 09/Apr/21
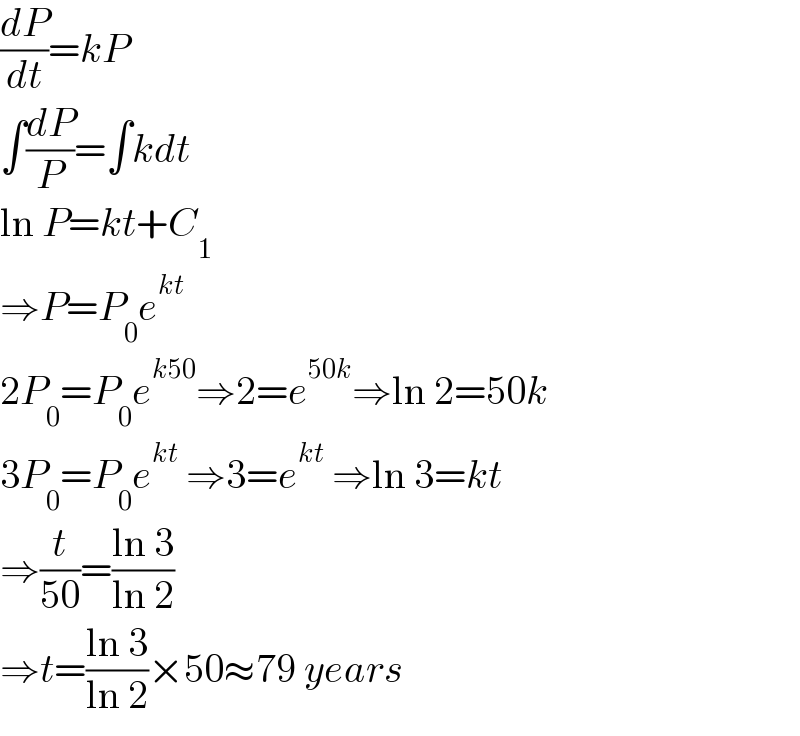
$$\frac{{dP}}{{dt}}={kP} \\ $$$$\int\frac{{dP}}{{P}}=\int{kdt} \\ $$$$\mathrm{ln}\:{P}={kt}+{C}_{\mathrm{1}} \\ $$$$\Rightarrow{P}={P}_{\mathrm{0}} {e}^{{kt}} \\ $$$$\mathrm{2}{P}_{\mathrm{0}} ={P}_{\mathrm{0}} {e}^{{k}\mathrm{50}} \Rightarrow\mathrm{2}={e}^{\mathrm{50}{k}} \Rightarrow\mathrm{ln}\:\mathrm{2}=\mathrm{50}{k} \\ $$$$\mathrm{3}{P}_{\mathrm{0}} ={P}_{\mathrm{0}} {e}^{{kt}} \:\Rightarrow\mathrm{3}={e}^{{kt}} \:\Rightarrow\mathrm{ln}\:\mathrm{3}={kt} \\ $$$$\Rightarrow\frac{{t}}{\mathrm{50}}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\Rightarrow{t}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}}×\mathrm{50}\approx\mathrm{79}\:{years} \\ $$
Commented by greg_ed last updated on 09/Apr/21

$$\boldsymbol{\mathrm{well}}\:\boldsymbol{\mathrm{done}}\:! \\ $$
Answered by Dwaipayan Shikari last updated on 09/Apr/21
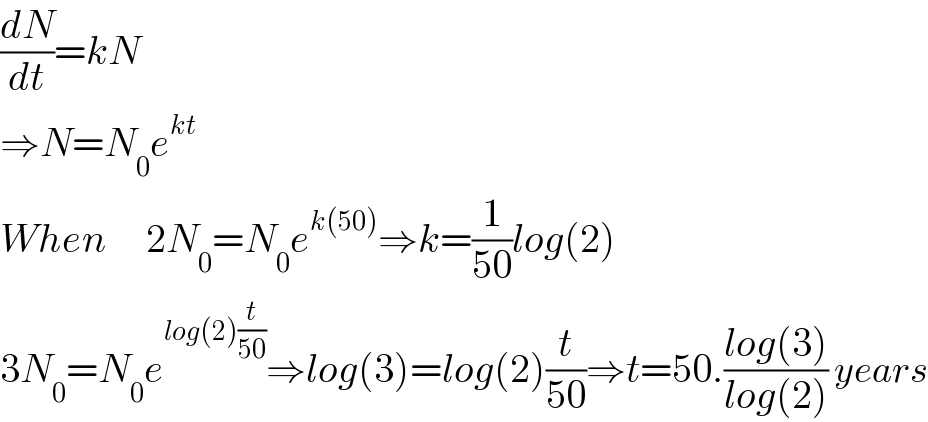
$$\frac{{dN}}{{dt}}={kN} \\ $$$$\Rightarrow{N}={N}_{\mathrm{0}} {e}^{{kt}} \\ $$$${When}\:\:\:\:\:\mathrm{2}{N}_{\mathrm{0}} ={N}_{\mathrm{0}} {e}^{{k}\left(\mathrm{50}\right)} \Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{50}}{log}\left(\mathrm{2}\right) \\ $$$$\mathrm{3}{N}_{\mathrm{0}} ={N}_{\mathrm{0}} {e}^{{log}\left(\mathrm{2}\right)\frac{{t}}{\mathrm{50}}} \Rightarrow{log}\left(\mathrm{3}\right)={log}\left(\mathrm{2}\right)\frac{{t}}{\mathrm{50}}\Rightarrow{t}=\mathrm{50}.\frac{{log}\left(\mathrm{3}\right)}{{log}\left(\mathrm{2}\right)}\:{years} \\ $$
