study-the-convergence-of-1-arctan-x-1-x-2-1-4-3-dx-

Question Number 66349 by mathmax by abdo last updated on 12/Aug/19

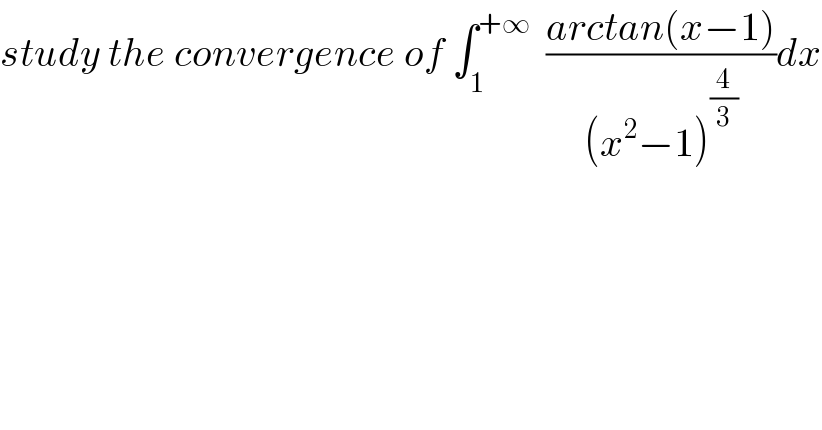
s t u d y t h e c o n v e r g e n c e o f \int_{1}^{+ \infty} \frac{a r c t a n (x - 1)}{{(x^{2} - 1)}^{\frac{4}{3}}} d x

Commented by mathmax by abdo last updated on 14/Aug/19

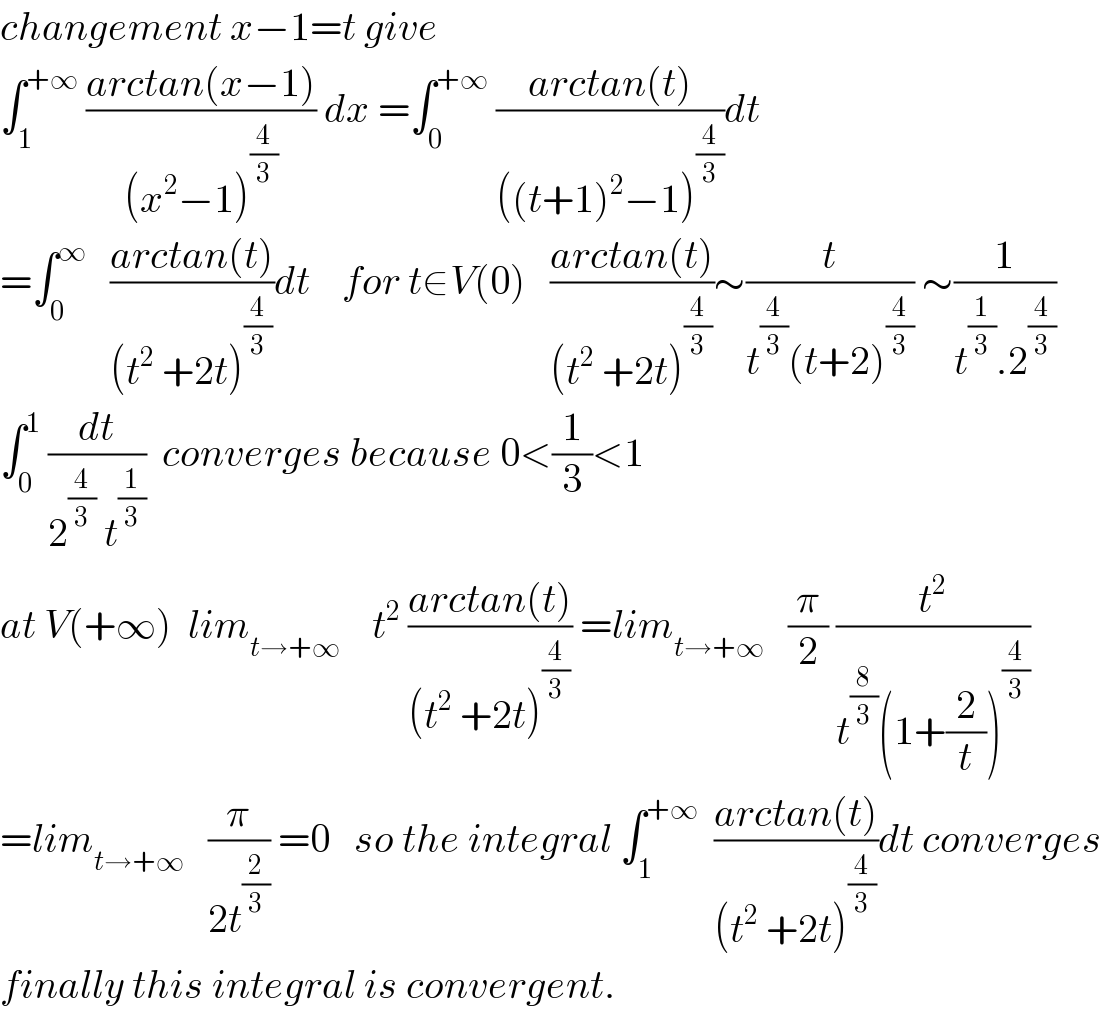
c h a n g e m e n t x - 1 = t g i v e

\int_{1}^{+ \infty} \frac{a r c t a n (x - 1)}{{(x^{2} - 1)}^{\frac{4}{3}}} d x = \int_{0}^{+ \infty} \frac{a r c t a n (t)}{{({(t + 1)}^{2} - 1)}^{\frac{4}{3}}} d t

= \int_{0}^{\infty} \frac{a r c t a n (t)}{{(t^{2} + 2 t)}^{\frac{4}{3}}} d t f o r t \in V (0) \frac{a r c t a n (t)}{{(t^{2} + 2 t)}^{\frac{4}{3}}} \sim \frac{t}{t^{\frac{4}{3}} {(t + 2)}^{\frac{4}{3}}} \sim \frac{1}{t^{\frac{1}{3}} . 2^{\frac{4}{3}}}

\int_{0}^{1} \frac{d t}{2^{\frac{4}{3}} t^{\frac{1}{3}}} c o n v e r g e s b e c a u s e 0 < \frac{1}{3} < 1

a t V (+ \infty) {l i m}_{t \to + \infty} t^{2} \frac{a r c t a n (t)}{{(t^{2} + 2 t)}^{\frac{4}{3}}} = {l i m}_{t \to + \infty} \frac{π}{2} \frac{t^{2}}{t^{\frac{8}{3}} {(1 + \frac{2}{t})}^{\frac{4}{3}}}

= {l i m}_{t \to + \infty} \frac{π}{2 t^{\frac{2}{3}}} = 0 s o t h e i n t e g r a l \int_{1}^{+ \infty} \frac{a r c t a n (t)}{{(t^{2} + 2 t)}^{\frac{4}{3}}} d t c o n v e r g e s

f i n a l l y t h i s i n t e g r a l i s c o n v e r g e n t .