Question Number 6328 by Rasheed Soomro last updated on 24/Jun/16

$$\mathrm{Sum}\:\mathrm{0}.\mathrm{7}+\mathrm{0}.\mathrm{71}+\mathrm{0}.\mathrm{72}+….\mathrm{to}\:\mathrm{100}\:\mathrm{terms}. \\ $$
Commented by FilupSmith last updated on 24/Jun/16
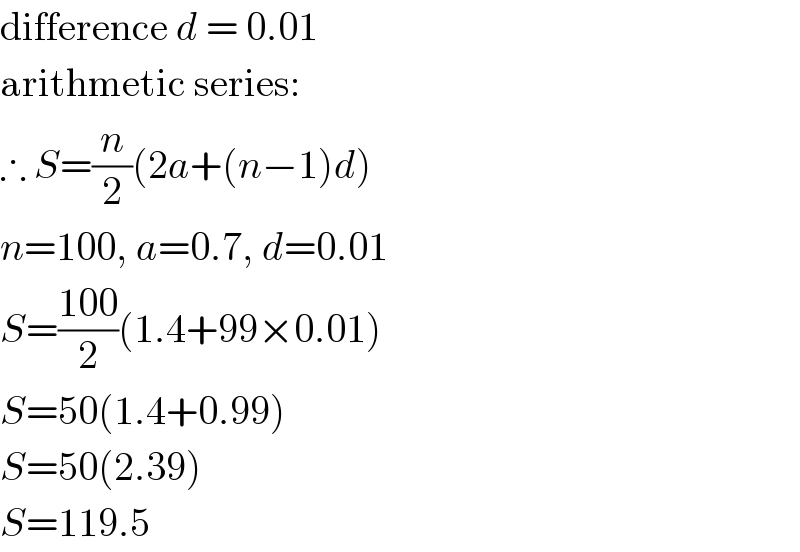
$$\mathrm{difference}\:{d}\:=\:\mathrm{0}.\mathrm{01} \\ $$$$\mathrm{arithmetic}\:\mathrm{series}: \\ $$$$\therefore\:{S}=\frac{{n}}{\mathrm{2}}\left(\mathrm{2}{a}+\left({n}−\mathrm{1}\right){d}\right) \\ $$$${n}=\mathrm{100},\:{a}=\mathrm{0}.\mathrm{7},\:{d}=\mathrm{0}.\mathrm{01} \\ $$$${S}=\frac{\mathrm{100}}{\mathrm{2}}\left(\mathrm{1}.\mathrm{4}+\mathrm{99}×\mathrm{0}.\mathrm{01}\right) \\ $$$${S}=\mathrm{50}\left(\mathrm{1}.\mathrm{4}+\mathrm{0}.\mathrm{99}\right) \\ $$$${S}=\mathrm{50}\left(\mathrm{2}.\mathrm{39}\right) \\ $$$${S}=\mathrm{119}.\mathrm{5} \\ $$
