Menu Close

Sum-the-following-series-to-infinity-1-1-k-x-1-k-k-2-x-2-x-and-k-being-proper-fractions-

Tinku Tara 0 Comments
Pin




Question Number 5427 by Rasheed Soomro last updated on 14/May/16
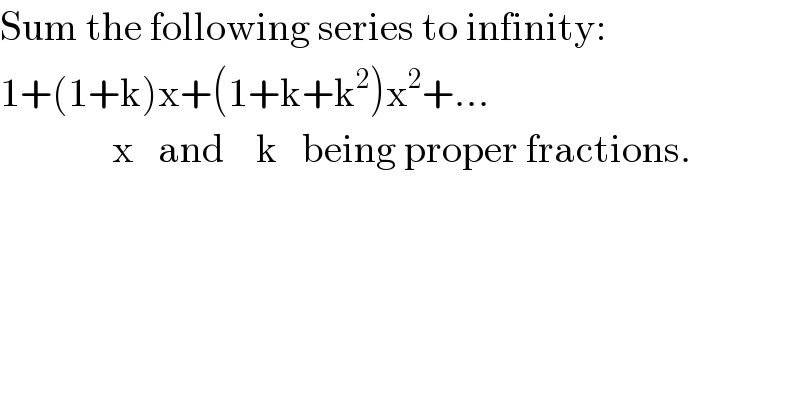
Sum the following series to infinity: 1+(1+k)x+(1+k+k^2 )x^2 +... x and k being proper fractions.
$$\mathrm{Sum}\:\mathrm{the}\:\mathrm{following}\:\mathrm{series}\:\mathrm{to}\:\mathrm{infinity}: \\ $$$$\mathrm{1}+\left(\mathrm{1}+\mathrm{k}\right)\mathrm{x}+\left(\mathrm{1}+\mathrm{k}+\mathrm{k}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} +… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:\:\:\mathrm{and}\:\:\:\:\mathrm{k}\:\:\:\mathrm{being}\:\mathrm{proper}\:\mathrm{fractions}. \\ $$
Commented by Yozzii last updated on 14/May/16
Let s=1+(1+k)x+(1+k+k^2 )x^2 +... Since k^(r+1) −1=(k−1)(1+k+k^2 +k^3 +...+k^r ) ⇒1−k^(r+1) =(1−k)(1+k+k^2 +...+k^r ) ⇒((1−k^(r+1) )/(1−k))=Σ_(j=0) ^r k^j (k∈F⇒k≠1) ∴ r=0⇒((1−k)/(1−k))=1 r=1⇒((1−k^2 )/(1−k))=1+k and so on. ∴ s=lim_(n→∞) (Σ_(r=0) ^n ((1−k^(r+1) )/(1−k))x^r ) (k∈F⇒k≠1) s=(1/(1−k))lim_(n→∞) (Σ_(r=0) ^n x^r −k(kx)^r ) Since x and k are proper fractions ⇒{x^r }_(r=0) ^∞ and {(kx)^r }_(r=0) ^∞ are infinite,convergent geometric progressions ⇒lim_(n→∞) Σ_(r=0) ^n x^r =(1/(1−x)) and lim_(n→∞) Σ_(r=0) ^n (kx)^r =(1/(1−kx)) ⇒s=(1/(1−k))((1/(1−x))−(k/(1−kx))) s=((1−kx−k+kx)/((1−k)(1−x)(1−kx))) s=(1/((1−x)(1−kx))) 1+(k+1)x+(1+k+k^2 )x^2 +...=(1/((1−x)(1−kx))) (k≠1, x≠(1/k))
$${Let}\:{s}=\mathrm{1}+\left(\mathrm{1}+{k}\right){x}+\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} \right){x}^{\mathrm{2}} +… \\ $$$${Since}\:{k}^{{r}+\mathrm{1}} −\mathrm{1}=\left({k}−\mathrm{1}\right)\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} +{k}^{\mathrm{3}} +…+{k}^{{r}} \right) \\ $$$$\Rightarrow\mathrm{1}−{k}^{{r}+\mathrm{1}} =\left(\mathrm{1}−{k}\right)\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} +…+{k}^{{r}} \right) \\ $$$$\Rightarrow\frac{\mathrm{1}−{k}^{{r}+\mathrm{1}} }{\mathrm{1}−{k}}=\underset{{j}=\mathrm{0}} {\overset{{r}} {\sum}}{k}^{{j}} \:\:\:\left({k}\in\mathbb{F}\Rightarrow{k}\neq\mathrm{1}\right) \\ $$$$\therefore\:{r}=\mathrm{0}\Rightarrow\frac{\mathrm{1}−{k}}{\mathrm{1}−{k}}=\mathrm{1} \\ $$$${r}=\mathrm{1}\Rightarrow\frac{\mathrm{1}−{k}^{\mathrm{2}} }{\mathrm{1}−{k}}=\mathrm{1}+{k} \\ $$$${and}\:{so}\:{on}. \\ $$$$\therefore\:{s}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}−{k}^{{r}+\mathrm{1}} }{\mathrm{1}−{k}}{x}^{{r}} \right)\:\left({k}\in\mathbb{F}\Rightarrow{k}\neq\mathrm{1}\right) \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{1}−{k}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{r}} −{k}\left({kx}\right)^{{r}} \right) \\ $$$${Since}\:{x}\:{and}\:{k}\:{are}\:{proper}\:{fractions} \\ $$$$\Rightarrow\left\{{x}^{{r}} \right\}_{{r}=\mathrm{0}} ^{\infty} \:{and}\:\left\{\left({kx}\right)^{{r}} \right\}_{{r}=\mathrm{0}} ^{\infty} \:\:{are}\:{infinite},{convergent}\:{geometric}\: \\ $$$${progressions} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{r}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}\:{and}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\left({kx}\right)^{{r}} =\frac{\mathrm{1}}{\mathrm{1}−{kx}} \\ $$$$\Rightarrow{s}=\frac{\mathrm{1}}{\mathrm{1}−{k}}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}−\frac{{k}}{\mathrm{1}−{kx}}\right) \\ $$$${s}=\frac{\mathrm{1}−{kx}−{k}+{kx}}{\left(\mathrm{1}−{k}\right)\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{kx}\right)} \\ $$$${s}=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{kx}\right)} \\ $$$$\mathrm{1}+\left({k}+\mathrm{1}\right){x}+\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} \right){x}^{\mathrm{2}} +…=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{kx}\right)}\:\:\left({k}\neq\mathrm{1},\:{x}\neq\frac{\mathrm{1}}{{k}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 14/May/16
A novel approach!
$$\boldsymbol{\mathrm{A}}\:\boldsymbol{\mathrm{n}}\mathrm{ovel}\:\mathrm{approach}! \\ $$
Answered by nchejane last updated on 14/May/16
1+(1+k)x+(1+k+k^2 )x^2 +(1+k+k^2 +k^3 )x^3 +... =(1+x+x^2 +x^3 +...)+k(x+x^2 +x^3 +...)+k^2 (x^2 +x^3 +x^4 +...)+... =(1/(1−x))+k(x/(1−x))+k^2 (x^2 /(1−x))+k^3 (x^3 /(1−x))+...(since abs(x)<1 ) =(1/(1−x))[1+kx+(kx)^2 +(kx)^3 +...] =(1/(1−x))×(1/(1−kx)) (since abs(kx)<1)
$$\mathrm{1}+\left(\mathrm{1}+{k}\right){x}+\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\left(\mathrm{1}+{k}+{k}^{\mathrm{2}} +{k}^{\mathrm{3}} \right){x}^{\mathrm{3}} +… \\ $$$$=\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right)+{k}\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right)+{k}^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +…\right)+… \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}+{k}\frac{{x}}{\mathrm{1}−{x}}+{k}^{\mathrm{2}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}}+{k}^{\mathrm{3}} \frac{{x}^{\mathrm{3}} }{\mathrm{1}−{x}}+…\left({since}\:{abs}\left({x}\right)<\mathrm{1}\:\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}\left[\mathrm{1}+{kx}+\left({kx}\right)^{\mathrm{2}} +\left({kx}\right)^{\mathrm{3}} +…\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{x}}×\frac{\mathrm{1}}{\mathrm{1}−{kx}}\:\:\left({since}\:{abs}\left({kx}\right)<\mathrm{1}\right) \\ $$
Commented by Rasheed Soomro last updated on 14/May/16
Nice approach!
$$\boldsymbol{\mathrm{N}}\mathrm{ice}\:\boldsymbol{\mathrm{a}}\mathrm{pproach}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *