Question Number 2159 by Yozzis last updated on 05/Nov/15
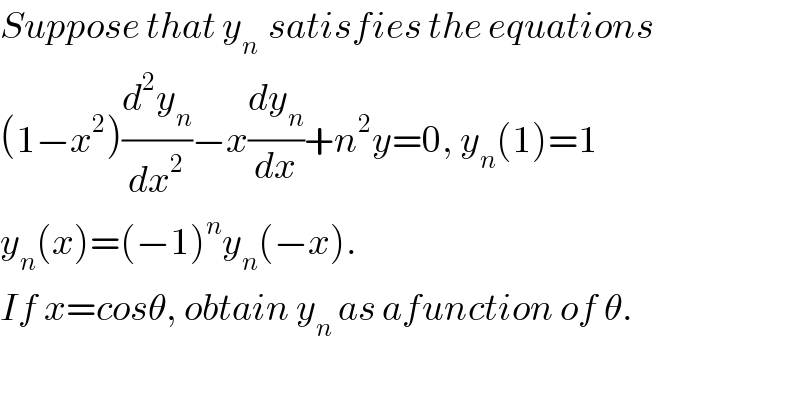
$${Suppose}\:{that}\:{y}_{{n}\:} \:{satisfies}\:{the}\:{equations}\: \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{d}^{\mathrm{2}} {y}_{{n}} }{{dx}^{\mathrm{2}} }−{x}\frac{{dy}_{{n}} }{{dx}}+{n}^{\mathrm{2}} {y}=\mathrm{0},\:{y}_{{n}} \left(\mathrm{1}\right)=\mathrm{1} \\ $$$${y}_{{n}} \left({x}\right)=\left(−\mathrm{1}\right)^{{n}} {y}_{{n}} \left(−{x}\right). \\ $$$${If}\:{x}={cos}\theta,\:{obtain}\:{y}_{{n}} \:{as}\:{afunction}\:{of}\:\theta. \\ $$
Answered by sudhanshur last updated on 06/Nov/15
![Chebyshev Equation in y_n y_n (x)=c_1 cosh[nln (x+(√(x^2 −1)))]+ic_2 sinh[nln (x+(√(x^2 −1)))] y_n (1)=1 c_1 cosh 0+ic_2 sinh 0=1 c_1 =1 y_n (−x)=(−1)^n y_n (x) x=cos θ ln (cos θ+isin θ)=ln e^(iθ) =iθ y_n (θ)=c_1 cosh (niθ)+ic_2 sinh (niθ) y_n =c_1 cos (nθ)−c_2 sin (nθ) y_n =cos (nθ)−c_2 sin (nθ)](https://www.tinkutara.com/question/Q2170.png)
$$\mathrm{Chebyshev}\:\mathrm{Equation}\:\mathrm{in}\:{y}_{{n}} \\ $$$${y}_{{n}} \left({x}\right)={c}_{\mathrm{1}} \mathrm{cosh}\left[{n}\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\right]+{ic}_{\mathrm{2}} \mathrm{sinh}\left[{n}\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\right] \\ $$$${y}_{{n}} \left(\mathrm{1}\right)=\mathrm{1} \\ $$$${c}_{\mathrm{1}} \mathrm{cosh}\:\mathrm{0}+{ic}_{\mathrm{2}} \mathrm{sinh}\:\mathrm{0}=\mathrm{1} \\ $$$${c}_{\mathrm{1}} =\mathrm{1} \\ $$$${y}_{{n}} \left(−{x}\right)=\left(−\mathrm{1}\right)^{{n}} {y}_{{n}} \left({x}\right) \\ $$$${x}=\mathrm{cos}\:\theta \\ $$$$\mathrm{ln}\:\left(\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta\right)=\mathrm{ln}\:{e}^{{i}\theta} ={i}\theta \\ $$$${y}_{{n}} \left(\theta\right)={c}_{\mathrm{1}} \mathrm{cosh}\:\left({ni}\theta\right)+{ic}_{\mathrm{2}} \mathrm{sinh}\:\left({ni}\theta\right) \\ $$$${y}_{{n}} ={c}_{\mathrm{1}} \mathrm{cos}\:\left({n}\theta\right)−{c}_{\mathrm{2}} \mathrm{sin}\:\left({n}\theta\right) \\ $$$${y}_{{n}} =\mathrm{cos}\:\left({n}\theta\right)−{c}_{\mathrm{2}} \mathrm{sin}\:\left({n}\theta\right) \\ $$
Commented by Yozzi last updated on 06/Nov/15

$${Sorry}.\:{I}\:{meant}\:{that}\:{one}\:{use}\:{the}\: \\ $$$${substitution}\:{x}={cos}\theta\:{to}\:{solve}\:{the} \\ $$$${d}.{e}\:{in}\:\theta\:{given}\:{the}\:{conditions}\:{are}\:{satisfied}. \\ $$$${I}\:{hadn}'{t}\:{known},\:{however},\:{that}\:{this} \\ $$$${is}\:{a}\:{special}\:{kind}\:{of}\:{d}.{e}\:{whose}\: \\ $$$${general}\:{solution}\:{could}\:{be}\:{quoted}.\: \\ $$$${I}'{m}\:{glad}\:{you}'{ve}\:{shared}\:{this}\:{knowledge}. \\ $$
