Question Number 77033 by necxxx last updated on 02/Jan/20

$${Suppose}\:{the}\:{population}\:{models}\:{of}\:{London} \\ $$$${and}\:{Hongkong}\:{in}\:{tens}\:{of}\:{thousands}\:{are} \\ $$$${p}\left({t}\right)=\frac{\mathrm{20}{t}}{{t}+\mathrm{1}}\:{and}\:{q}\left({t}\right)=\frac{\mathrm{240}{t}}{{t}+\mathrm{8}}\:{respectively}\:{for} \\ $$$${t}\:{years}\:{after}\:\mathrm{2015},\:{Determine}\:{the}\:{time}\:{period} \\ $$$${in}\:{years}\:{when}\:{the}\:{population}\:{of}\:{London} \\ $$$${exceeds}\:{that}\:{of}\:{HongKong}. \\ $$
Commented by MJS last updated on 02/Jan/20
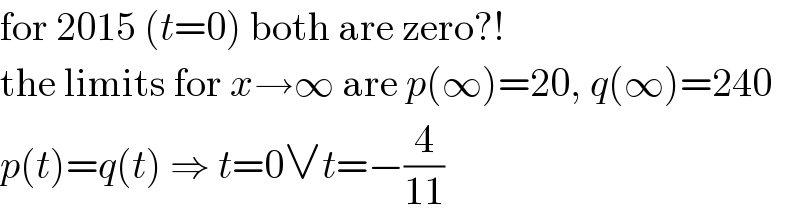
$$\mathrm{for}\:\mathrm{2015}\:\left({t}=\mathrm{0}\right)\:\mathrm{both}\:\mathrm{are}\:\mathrm{zero}?! \\ $$$$\mathrm{the}\:\mathrm{limits}\:\mathrm{for}\:{x}\rightarrow\infty\:\mathrm{are}\:{p}\left(\infty\right)=\mathrm{20},\:{q}\left(\infty\right)=\mathrm{240} \\ $$$${p}\left({t}\right)={q}\left({t}\right)\:\Rightarrow\:{t}=\mathrm{0}\vee{t}=−\frac{\mathrm{4}}{\mathrm{11}} \\ $$
