Question Number 142103 by rs4089 last updated on 26/May/21
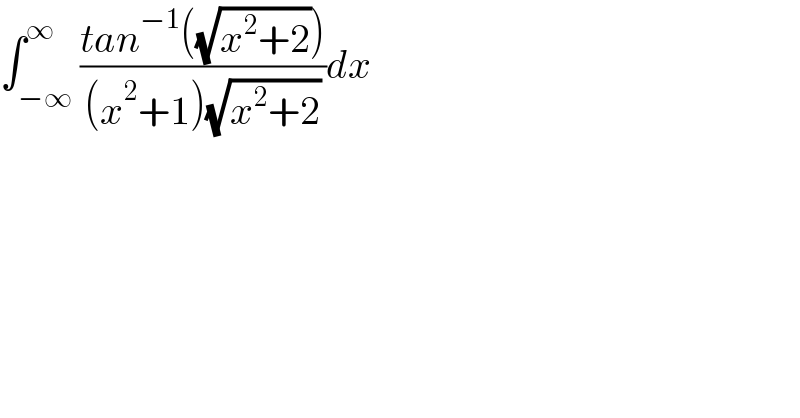
$$\int_{−\infty} ^{\infty} \frac{{tan}^{−\mathrm{1}} \left(\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}{dx} \\ $$
Answered by mathmax by abdo last updated on 26/May/21
![f(a)=∫_(−∞) ^(+∞) ((arctan(a(√(x^2 +2))))/((x^2 +1)(√(x^2 +2))))dx ⇒ f^′ (a)=∫_(−∞) ^(+∞) (dx/((x^2 +1)(1+a^2 (x^2 +2))))=2∫_0 ^∞ (dx/((x^2 +1)(a^2 x^2 +2a^2 +1))) =_(ax=t) 2∫_0 ^∞ (dt/(a((t^2 /a^2 )+1)(t^2 +2a^2 +1))) =2a∫_0 ^∞ (dt/((t^2 +a^2 )(t^2 +2a^2 +1))) =((2a)/(a^2 +1))∫_0 ^∞ ((1/(t^2 +a^2 ))−(1/(t^2 +2a^2 +1)))dt =((2a)/(a^2 +1)){ ∫_0 ^∞ (dt/(t^2 +a^2 ))−∫_0 ^∞ (dt/(t^2 +2a^2 +1))} we have ∫_0 ^∞ (dt/(t^2 +a^2 ))=_(t=ay) ∫_0 ^∞ ((ady)/(a^2 (y^2 +1)))=(1/a)arctan((t/a))]_0 ^∞ =(π/(2a)) ∫_0 ^∞ (dt/(t^2 +2a^2 +1)) =_(t=(√(2a^2 +1))y) ∫_0 ^∞ ((√(2a^2 +1))/((2a^2 +1)(y^2 +1)))dy =(1/( (√(2a^2 +1)))) arctan((t/( (√(2a^2 +1)))))]_0 ^∞ =(π/(2(√(2a^2 +1)))) f^′ (a)=((2a)/(a^2 +1))(π/(2a))−((2a)/(a^2 +1))(π/(2(√(2a^2 +1))))=(π/(a^2 +1))−((aπ)/((a^2 +1)(√(2a^2 +1)))) ⇒ f(a)=π ∫_0 ^a (dx/(x^2 +1))−π ∫_0 ^a ((xdx)/((x^2 +1)(√(2x^2 +1)))) +C f(0)=0=C ⇒f(a)=π∫_0 ^a (dx/(x^2 +1))−π ∫_0 ^a ((xdx)/((x^2 +1)(√(2x^2 +1)))) and ∫_(−∞) ^(+∞) ((arctan((√(x^2 +2))))/((x^2 +1)(√(x^2 +2))))dx=f(1)=π∫_0 ^1 (dx/(x^2 +1))−π∫_0 ^1 ((xdx)/((x^2 +1)(√(2x^2 +1)))) we have ∫_0 ^1 (dx/(x^2 +1))=(π/4) ∫_0 ^1 ((xdx)/((x^2 +1)(√(2x^2 +1)))) =_((√2)x=shy) ∫_0 ^(argsh((√2))) ((shy)/( (√2)(((sh^2 y)/2)+1)chy))((chy)/( (√2)))dy =(1/2)∫_0 ^(log((√2)+(√3))) ((shy)/((1/2)sh^2 y +1))dy =∫_0 ^(log((√2)+(√3))) ((shy)/(sh^2 y +2))dy =∫_0 ^(log((√2)+(√3))) ((shy)/(((ch(2y)−1)/2)+2))dy=2∫_0 ^(log((√2)+(√3))) ((shy)/(ch(2y)+3))dy =2∫_0 ^(log((√2)+(√3))) (((e^y −e^(−y) )/2)/(((e^(2y) −e^(−2y) )/2)+3))dy=2∫_0 ^(log((√2)+(√3))) ((e^y −e^(−y) )/(e^(2y) −e^(−2y) +6))dy =2 ∫_0 ^(log((√2)+(√3))) ((e^(3y) −e^y )/(e^(4y) −1+6e^(2y) ))dy =_(e^y =u) 2∫_1 ^((√2)+(√3)) ((u^3 −u)/(u^4 +6u^2 −1))(du/u) =2 ∫_1 ^((√2)+(√3)) ((u^2 −1)/(u^4 +6u^2 −1))du u^4 +6u^2 −1=0 ⇒z^2 +6z−1=0 (z=u^2 ) Δ^′ =9+1=10 ⇒u_1 =−3+(√(10)) and u_2 =−3−(√(10)) u^4 +6u^2 −1 =(u^2 −u_1 )(u^2 −u_2 ) ⇒ Ψ(u)=((u^2 −1)/(u^4 +6u^2 −1))=(u^2 −1)((1/(u^2 −u_1 ))−(1/(u^2 −u_2 )))×(1/(u_1 −u_2 )) =(1/(2(√(10))))(((u^2 −1)/(u^2 −u_1 ))−((u^2 −1)/(u^2 −u_2 ))) =(1/(2(√(10))))(((u^2 −u_1 +u_1 −1)/(u^2 −u_1 ))−((u^2 −u_2 +u_2 −1)/(u^2 −u_2 ))) =(1/(2(√(10))))(((u_1 −1)/(u^2 −u_1 ))−((u_2 −1)/(u^2 −u_2 ))) ⇒ ∫_0 ^1 ((xdx)/((x^2 +1)(√(2x^2 +1))))=((u_1 −1)/( (√(10))))∫_1 ^((√2)+(√3)) (du/(u^2 −u_1 ))−((u_2 −1)/( (√(10))))∫_1 ^((√2)+(√3)) (du/(u^2 −u_2 )) now its eazy to find those integrals....](https://www.tinkutara.com/question/Q142110.png)
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{arctan}\left(\mathrm{a}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)\right)}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \:+\mathrm{2a}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=_{\mathrm{ax}=\mathrm{t}} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{a}\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{2a}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\mathrm{2a}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2a}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2a}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \:\:\left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{2a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\left\{\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}\right\}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left.\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }=_{\mathrm{t}=\mathrm{ay}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ady}}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{arctan}\left(\frac{\mathrm{t}}{\mathrm{a}}\right)\right]_{\mathrm{0}} ^{\infty} \:=\frac{\pi}{\mathrm{2a}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{2a}^{\mathrm{2}} \:+\mathrm{1}}\:=_{\mathrm{t}=\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}\mathrm{y}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}}{\left(\mathrm{2a}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dy} \\ $$$$\left.=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}}\:\mathrm{arctan}\left(\frac{\mathrm{t}}{\:\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\mathrm{2a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\frac{\pi}{\mathrm{2a}}−\frac{\mathrm{2a}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2a}^{\mathrm{2}} \:+\mathrm{1}}}=\frac{\pi}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{a}\pi}{\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{\mathrm{2a}^{\mathrm{2}} +\mathrm{1}}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\pi\:\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}−\pi\:\int_{\mathrm{0}} ^{\mathrm{a}} \:\:\:\frac{\mathrm{xdx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}}}\:+\mathrm{C} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}=\mathrm{C}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\pi\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\pi\:\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{xdx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$$\mathrm{and}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{arctan}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2}}}\mathrm{dx}=\mathrm{f}\left(\mathrm{1}\right)=\pi\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\pi\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xdx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xdx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}}}\:=_{\sqrt{\mathrm{2}}\mathrm{x}=\mathrm{shy}} \:\:\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\sqrt{\mathrm{2}}\right)} \:\frac{\mathrm{shy}}{\:\sqrt{\mathrm{2}}\left(\frac{\mathrm{sh}^{\mathrm{2}} \mathrm{y}}{\mathrm{2}}+\mathrm{1}\right)\mathrm{chy}}\frac{\mathrm{chy}}{\:\sqrt{\mathrm{2}}}\mathrm{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{log}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)} \:\frac{\mathrm{shy}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}^{\mathrm{2}} \mathrm{y}\:+\mathrm{1}}\mathrm{dy}\:=\int_{\mathrm{0}} ^{\mathrm{log}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)} \:\frac{\mathrm{shy}}{\mathrm{sh}^{\mathrm{2}} \mathrm{y}\:+\mathrm{2}}\mathrm{dy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{log}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)} \:\frac{\mathrm{shy}}{\frac{\mathrm{ch}\left(\mathrm{2y}\right)−\mathrm{1}}{\mathrm{2}}+\mathrm{2}}\mathrm{dy}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{log}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)} \:\frac{\mathrm{shy}}{\mathrm{ch}\left(\mathrm{2y}\right)+\mathrm{3}}\mathrm{dy} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{log}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)} \:\:\:\:\frac{\frac{\mathrm{e}^{\mathrm{y}} −\mathrm{e}^{−\mathrm{y}} }{\mathrm{2}}}{\frac{\mathrm{e}^{\mathrm{2y}} −\mathrm{e}^{−\mathrm{2y}} }{\mathrm{2}}+\mathrm{3}}\mathrm{dy}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{log}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)} \:\frac{\mathrm{e}^{\mathrm{y}} −\mathrm{e}^{−\mathrm{y}} }{\mathrm{e}^{\mathrm{2y}} −\mathrm{e}^{−\mathrm{2y}} +\mathrm{6}}\mathrm{dy} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{log}\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)} \:\frac{\mathrm{e}^{\mathrm{3y}} −\mathrm{e}^{\mathrm{y}} }{\mathrm{e}^{\mathrm{4y}} −\mathrm{1}+\mathrm{6e}^{\mathrm{2y}} }\mathrm{dy} \\ $$$$=_{\mathrm{e}^{\mathrm{y}} \:=\mathrm{u}} \:\:\:\mathrm{2}\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{u}^{\mathrm{3}} −\mathrm{u}}{\mathrm{u}^{\mathrm{4}} +\mathrm{6u}^{\mathrm{2}} −\mathrm{1}}\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}} \:\:\:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{4}} +\mathrm{6u}^{\mathrm{2}} −\mathrm{1}}\mathrm{du} \\ $$$$\mathrm{u}^{\mathrm{4}} +\mathrm{6u}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{z}^{\mathrm{2}} +\mathrm{6z}−\mathrm{1}=\mathrm{0}\:\:\left(\mathrm{z}=\mathrm{u}^{\mathrm{2}} \right) \\ $$$$\Delta^{'} \:=\mathrm{9}+\mathrm{1}=\mathrm{10}\:\Rightarrow\mathrm{u}_{\mathrm{1}} =−\mathrm{3}+\sqrt{\mathrm{10}}\:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =−\mathrm{3}−\sqrt{\mathrm{10}} \\ $$$$\mathrm{u}^{\mathrm{4}} +\mathrm{6u}^{\mathrm{2}} \:−\mathrm{1}\:=\left(\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} \right)\left(\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\Psi\left(\mathrm{u}\right)=\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{4}} +\mathrm{6u}^{\mathrm{2}} −\mathrm{1}}=\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right)×\frac{\mathrm{1}}{\mathrm{u}_{\mathrm{1}} −\mathrm{u}_{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{10}}}\left(\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right)\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{10}}}\left(\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} +\mathrm{u}_{\mathrm{1}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} +\mathrm{u}_{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{10}}}\left(\frac{\mathrm{u}_{\mathrm{1}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{u}_{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{xdx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\sqrt{\mathrm{2x}^{\mathrm{2}} +\mathrm{1}}}=\frac{\mathrm{u}_{\mathrm{1}} −\mathrm{1}}{\:\sqrt{\mathrm{10}}}\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}} \:\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{1}} }−\frac{\mathrm{u}_{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{10}}}\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} −\mathrm{u}_{\mathrm{2}} } \\ $$$$\mathrm{now}\:\mathrm{its}\:\mathrm{eazy}\:\mathrm{to}\:\mathrm{find}\:\mathrm{those}\:\mathrm{integrals}…. \\ $$
Answered by mindispower last updated on 26/May/21
![∫_(−∞) ^∞ ((tan^− (t(√(x^2 +2))))/( (√(x^2 +2))(1+x^2 )))dx=f(t) f′(t)=∫_(−∞) ^∞ (1/((1+x^2 )(1+2t^2 +t^2 x^2 ))) =2iπ.((1/(2i(1+t^2 )))+(1/(1−((1+2t^2 )/t^2 ))).(1/(2it(√(1+2t^2 ))))) =(π/(1+t^2 ))+((πt)/(−(1+t^2 )(√(1+2t^2 ))))=f′(t) f(0)=0⇔∫_(−∞) ^∞ ((arctan((√(x^2 +2))))/((1+x^2 )(√(x^2 +2)))) dx=f(1)=∫_0 ^1 f′(t)dt =∫_0 ^1 (π/(1+t^2 ))−(π/2)∫_0 ^1 (dx/((1+x)(√(1+2x))))dx =(π^2 /4)−(π/2)∫_1 ^3 ((udu)/(((u^2 +1)/2)u))=(π^2 /4)−π∫_1 ^(√3) (du/((u^2 +1))) =(π^2 /4)−π[_1 ^(√3) arctan(u)] =(π^2 /4)−π.(π/(12))=(π^2 /6) ∫_(−∞) ^∞ ((tan^(−1) ((√(2x+1))))/((1+x^2 )(√(2x+1))))dx=(π^2 /6)](https://www.tinkutara.com/question/Q142139.png)
$$\int_{−\infty} ^{\infty} \frac{{tan}^{−} \left({t}\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\right)}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}={f}\left({t}\right) \\ $$$${f}'\left({t}\right)=\int_{−\infty} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} +{t}^{\mathrm{2}} {x}^{\mathrm{2}} \right)} \\ $$$$=\mathrm{2}{i}\pi.\left(\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{2}{it}\sqrt{\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} }}\right) \\ $$$$=\frac{\pi}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\pi{t}}{−\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} }}={f}'\left({t}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Leftrightarrow\int_{−\infty} ^{\infty} \frac{{arctan}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}\:{dx}={f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {f}'\left({t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\pi}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}+{x}\right)\sqrt{\mathrm{1}+\mathrm{2}{x}}}{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\frac{\pi}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{3}} \frac{{udu}}{\frac{{u}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}{u}}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\pi\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \frac{{du}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\pi\left[_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} {arctan}\left({u}\right)\right] \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\pi.\frac{\pi}{\mathrm{12}}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\int_{−\infty} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}{x}+\mathrm{1}}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{2}{x}+\mathrm{1}}}{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$
