Menu Close

tan-2-x-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 70917 by Kunal12588 last updated on 09/Oct/19
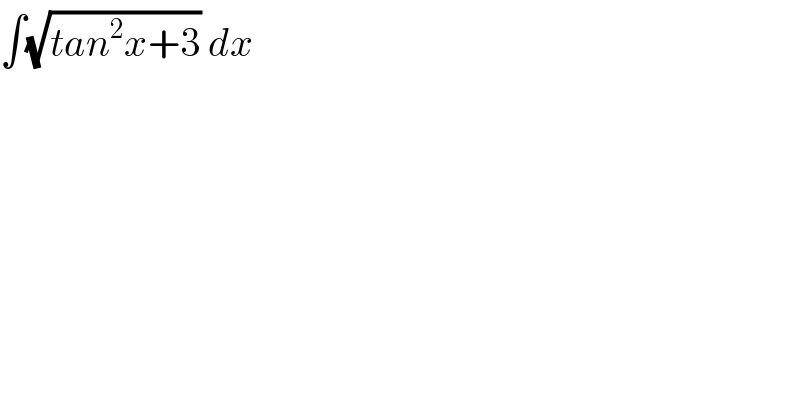
∫(√(tan^2 x+3)) dx
$$\int\sqrt{{tan}^{\mathrm{2}} {x}+\mathrm{3}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 09/Oct/19
(√3)t=tanx ⇒x=arctan(t(√3))) ⇒ ∫(√(3+tan^2 x))dx =(√3)∫ (√(1+t^2 ))((√3)/(1+3t^2 ))dt =3 ∫((√(1+t^2 ))/(1+3t^2 ))dt changement t=sh(u) give ∫((√(1+t^2 ))/(1+3t^2 ))dt =∫((ch(u))/(1+3sh^2 u)) chu du =∫ (((1+ch(2u))/2)/(1+3((ch(2u)−1)/2)))du =∫ ((1+ch(2u))/(2+3ch(2u)−3))du =∫((ch(2u)+1)/(3ch(2u)−1))du =∫ ((((e^(2u) +e^(−2u) )/2)+1)/(3((e^(2u) +e^(−2u) )/2)−1))du =∫((e^(2u) +e^(−2u) +2)/(3 e^(2u) +3e^(−2u) −2))du =_(e^(2u) =z) ∫ ((z+z^(−1) +2)/(3z +3z^(−1) −2))(dz/(2z)) =(1/2) ∫ ((z+z^(−1) +2)/(3z^2 +3−2z))dz =(1/2) ∫ ((z^2 +2z+1)/(z(3z^2 −2z +3)))dz let decompose F(z)=((z^2 +2z+1)/(z(3z^2 −2z +3))) 3z^2 −2z+3=0→Δ^′ =1−9<0 ⇒F(z)=(a/z) +((bz+c)/(3z^2 −2z +3)) a=(1/3) lim_(z→+∞) zF(z)=(1/3) =a+(b/3) ⇒1 =3a+b ⇒b=1−3a=0 ⇒ F(z)=(1/(3z)) +(c/(3z^2 −2z +3)) F(1)=(4/4)=1 =(1/3) +(c/4) ⇒4=(4/3) +c ⇒c=4−(4/3) =(8/3) ⇒ F(z)=(1/(3z)) +(8/(3(3z^2 −2z +3))) ⇒(1/2)∫F(z)dz=(1/6)ln∣z∣+(8/9) ∫ (dz/(z^2 −(2/3)z+1)) ∫ (dz/(z^2 −(2/3)z +1)) =∫ (dz/(z^2 −2(1/3)z +(1/9)+1−(1/9))) =∫ (dz/((z−(1/3))^2 +(8/9))) =_(z−(1/3)=((2(√2))/3)u) (9/8) ∫(1/(1+u^2 ))((2(√2))/3)du =((3(√2))/4) arctan(((3z−1)/(2(√2)))) +c=((3(√2))/4) arctan(((3e^(2u) −1)/(2(√2))))+c but u=argsh(t)=ln(t+(√(1+t^2 ))) ⇒2u=2ln(t+(√(1+t^2 ))) ⇒e^(2u) =(t+(√(1+t^2 ))) =(((tanx)/( (√3))) +(√(1+((tan^2 x)/3)))) ⇒ I =(1/(3((1/3)+((2(√2))/3)ln( ((tanx)/( (√3))) +(√(1+((tan^2 x)/3)))))) +((3(√2))/4) arctan(((3(((tanx)/( (√3)))+(√(1+((tan^2 x)/3)))−1)/(2(√2)))) + C.
$$\left.\sqrt{\mathrm{3}}{t}={tanx}\:\Rightarrow{x}={arctan}\left({t}\sqrt{\mathrm{3}}\right)\right)\:\Rightarrow \\ $$$$\int\sqrt{\mathrm{3}+{tan}^{\mathrm{2}} {x}}{dx}\:=\sqrt{\mathrm{3}}\int\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\frac{\sqrt{\mathrm{3}}}{\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} }{dt}\:=\mathrm{3}\:\int\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} }{dt} \\ $$$${changement}\:{t}={sh}\left({u}\right)\:{give} \\ $$$$\int\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} }{dt}\:=\int\frac{{ch}\left({u}\right)}{\mathrm{1}+\mathrm{3}{sh}^{\mathrm{2}} {u}}\:{chu}\:{du}\:=\int\:\:\frac{\frac{\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)}{\mathrm{2}}}{\mathrm{1}+\mathrm{3}\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}}}{du} \\ $$$$=\int\:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)}{\mathrm{2}+\mathrm{3}{ch}\left(\mathrm{2}{u}\right)−\mathrm{3}}{du}\:=\int\frac{{ch}\left(\mathrm{2}{u}\right)+\mathrm{1}}{\mathrm{3}{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{du} \\ $$$$=\int\:\:\frac{\frac{{e}^{\mathrm{2}{u}} +{e}^{−\mathrm{2}{u}} }{\mathrm{2}}+\mathrm{1}}{\mathrm{3}\frac{{e}^{\mathrm{2}{u}} +{e}^{−\mathrm{2}{u}} }{\mathrm{2}}−\mathrm{1}}{du}\:=\int\frac{{e}^{\mathrm{2}{u}} +{e}^{−\mathrm{2}{u}} \:+\mathrm{2}}{\mathrm{3}\:{e}^{\mathrm{2}{u}} \:+\mathrm{3}{e}^{−\mathrm{2}{u}} −\mathrm{2}}{du} \\ $$$$=_{{e}^{\mathrm{2}{u}} ={z}} \:\:\:\:\:\int\:\:\frac{{z}+{z}^{−\mathrm{1}} \:+\mathrm{2}}{\mathrm{3}{z}\:+\mathrm{3}{z}^{−\mathrm{1}} −\mathrm{2}}\frac{{dz}}{\mathrm{2}{z}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{{z}+{z}^{−\mathrm{1}} \:+\mathrm{2}}{\mathrm{3}{z}^{\mathrm{2}} \:+\mathrm{3}−\mathrm{2}{z}}{dz}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{{z}^{\mathrm{2}} \:+\mathrm{2}{z}+\mathrm{1}}{{z}\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}\:+\mathrm{3}\right)}{dz} \\ $$$${let}\:{decompose}\:{F}\left({z}\right)=\frac{{z}^{\mathrm{2}} \:+\mathrm{2}{z}+\mathrm{1}}{{z}\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}\:+\mathrm{3}\right)} \\ $$$$\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{3}=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{1}−\mathrm{9}<\mathrm{0}\:\Rightarrow{F}\left({z}\right)=\frac{{a}}{{z}}\:+\frac{{bz}+{c}}{\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}\:+\mathrm{3}} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${lim}_{{z}\rightarrow+\infty} {zF}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{3}}\:={a}+\frac{{b}}{\mathrm{3}}\:\Rightarrow\mathrm{1}\:=\mathrm{3}{a}+{b}\:\Rightarrow{b}=\mathrm{1}−\mathrm{3}{a}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{3}{z}}\:+\frac{{c}}{\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}\:+\mathrm{3}} \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{4}}{\mathrm{4}}=\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{{c}}{\mathrm{4}}\:\Rightarrow\mathrm{4}=\frac{\mathrm{4}}{\mathrm{3}}\:+{c}\:\Rightarrow{c}=\mathrm{4}−\frac{\mathrm{4}}{\mathrm{3}}\:=\frac{\mathrm{8}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{3}{z}}\:+\frac{\mathrm{8}}{\mathrm{3}\left(\mathrm{3}{z}^{\mathrm{2}} −\mathrm{2}{z}\:+\mathrm{3}\right)}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int{F}\left({z}\right){dz}=\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid{z}\mid+\frac{\mathrm{8}}{\mathrm{9}}\:\int\:\:\:\frac{{dz}}{{z}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{z}+\mathrm{1}} \\ $$$$\int\:\:\:\frac{{dz}}{{z}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{z}\:+\mathrm{1}}\:=\int\:\:\frac{{dz}}{{z}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{1}}{\mathrm{3}}{z}\:+\frac{\mathrm{1}}{\mathrm{9}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}}} \\ $$$$=\int\:\:\frac{{dz}}{\left({z}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{9}}}\:=_{{z}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}{u}} \:\frac{\mathrm{9}}{\mathrm{8}}\:\:\int\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}{du} \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\:{arctan}\left(\frac{\mathrm{3}{z}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\:+{c}=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\:{arctan}\left(\frac{\mathrm{3}{e}^{\mathrm{2}{u}} −\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)+{c}\:{but} \\ $$$${u}={argsh}\left({t}\right)={ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:\:\:\Rightarrow\mathrm{2}{u}=\mathrm{2}{ln}\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{e}^{\mathrm{2}{u}} \:=\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:\:\:=\left(\frac{{tanx}}{\:\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{3}}}\right)\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}{ln}\left(\:\frac{{tanx}}{\:\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{3}}}\right)\right.}\:+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\:{arctan}\left(\frac{\mathrm{3}\left(\frac{{tanx}}{\:\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\frac{{tan}^{\mathrm{2}} {x}}{\mathrm{3}}}−\mathrm{1}\right.}{\mathrm{2}\sqrt{\mathrm{2}}}\right) \\ $$$$+\:{C}. \\ $$
Commented by Kunal12588 last updated on 10/Oct/19
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 10/Oct/19
you are welcome.
$${you}\:{are}\:{welcome}. \\ $$
Answered by Kunal12588 last updated on 09/Oct/19
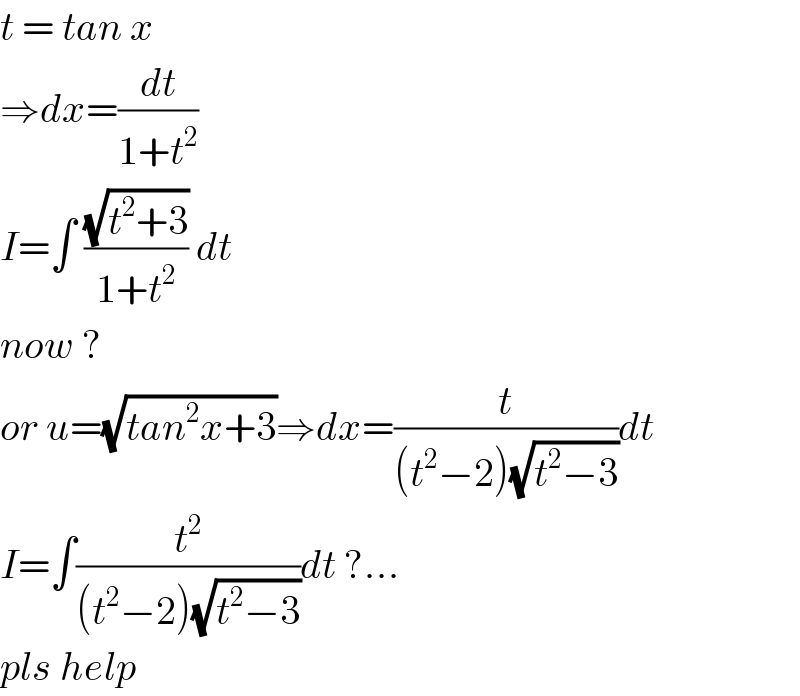
t = tan x ⇒dx=(dt/(1+t^2 )) I=∫ ((√(t^2 +3))/(1+t^2 )) dt now ? or u=(√(tan^2 x+3))⇒dx=(t/((t^2 −2)(√(t^2 −3))))dt I=∫(t^2 /((t^2 −2)(√(t^2 −3))))dt ?... pls help
$${t}\:=\:{tan}\:{x} \\ $$$$\Rightarrow{dx}=\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}=\int\:\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$${now}\:? \\ $$$${or}\:{u}=\sqrt{{tan}^{\mathrm{2}} {x}+\mathrm{3}}\Rightarrow{dx}=\frac{{t}}{\left({t}^{\mathrm{2}} −\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{3}}}{dt} \\ $$$${I}=\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{2}\right)\sqrt{{t}^{\mathrm{2}} −\mathrm{3}}}{dt}\:?… \\ $$$${pls}\:{help} \\ $$
Commented by MJS last updated on 09/Oct/19
easier ∫((√(t^2 +3))/(t^2 +1))dt= [u=(t/( (√(t^2 +3)))) → dt=((√((t^2 +3)^3 ))/3)] =−3∫(du/((u−1)(u+1)(2u^2 +1)))= =−(1/2)∫(du/(u−1))+(1/2)∫(du/(u+1))+2∫(du/(2u^2 +1))= =−(1/2)ln (u−1) +(1/2)ln (u+1) +(√2)tan^(−1) ((√2)u) = =(1/2)ln ((u+1)/(u−1)) +(√2)tan^(−1) ((√2)u) =...
$$\mathrm{easier} \\ $$$$\int\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}\:\rightarrow\:{dt}=\frac{\sqrt{\left({t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{3}} }}{\mathrm{3}}\right] \\ $$$$=−\mathrm{3}\int\frac{{du}}{\left({u}−\mathrm{1}\right)\left({u}+\mathrm{1}\right)\left(\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{{u}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{{u}+\mathrm{1}}+\mathrm{2}\int\frac{{du}}{\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({u}−\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({u}+\mathrm{1}\right)\:+\sqrt{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}{u}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{{u}+\mathrm{1}}{{u}−\mathrm{1}}\:+\sqrt{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}{u}\right)\:=… \\ $$$$ \\ $$
Commented by MJS last updated on 09/Oct/19
∫((√(t^2 +3))/(t^2 +1))dt= [u=sinh^(−1) (t/( (√3))) → dt=(√(t^2 +3))du] =3∫((e^(4u) +2e^(2u) +1)/(3e^(4u) −2e^(2u) +3))du= [v=e^(2u) → du=(dv/(2e^(2u) ))] =(3/2)∫(((v+1)^2 )/((3v^2 −2v+3)v))dv=(1/2)∫(dv/v)+4∫(dv/(3v^2 −2v+3))= =(1/2)ln v +(√2)tan^(−1) (((√2)(3v−1))/4) =...
$$\int\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{{t}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dt}=\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}{du}\right] \\ $$$$=\mathrm{3}\int\frac{\mathrm{e}^{\mathrm{4}{u}} +\mathrm{2e}^{\mathrm{2}{u}} +\mathrm{1}}{\mathrm{3e}^{\mathrm{4}{u}} −\mathrm{2e}^{\mathrm{2}{u}} +\mathrm{3}}{du}= \\ $$$$\:\:\:\:\:\left[{v}=\mathrm{e}^{\mathrm{2}{u}} \:\rightarrow\:{du}=\frac{{dv}}{\mathrm{2e}^{\mathrm{2}{u}} }\right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\left({v}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{3}{v}^{\mathrm{2}} −\mathrm{2}{v}+\mathrm{3}\right){v}}{dv}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dv}}{{v}}+\mathrm{4}\int\frac{{dv}}{\mathrm{3}{v}^{\mathrm{2}} −\mathrm{2}{v}+\mathrm{3}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{v}\:+\sqrt{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{2}}\left(\mathrm{3}{v}−\mathrm{1}\right)}{\mathrm{4}}\:=… \\ $$
Commented by Kunal12588 last updated on 10/Oct/19
thnaks a lot sir
$${thnaks}\:{a}\:{lot}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *