Question Number 143680 by mathlove last updated on 17/Jun/21

$$\mathrm{tan}\:\mathrm{76}=\mathrm{4} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{14}=? \\ $$
Commented by mr W last updated on 17/Jun/21
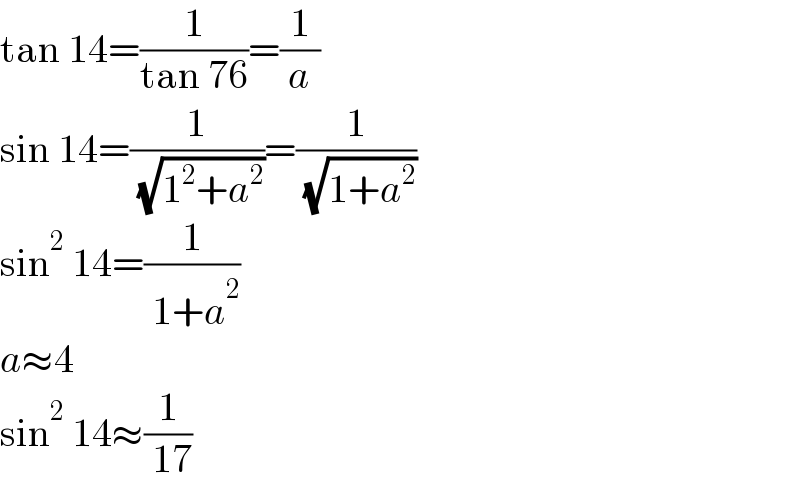
$$\mathrm{tan}\:\mathrm{14}=\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{76}}=\frac{\mathrm{1}}{{a}} \\ $$$$\mathrm{sin}\:\mathrm{14}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +{a}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{14}=\frac{\mathrm{1}}{\:\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$${a}\approx\mathrm{4} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{14}\approx\frac{\mathrm{1}}{\:\mathrm{17}} \\ $$
Answered by TheHoneyCat last updated on 17/Jun/21
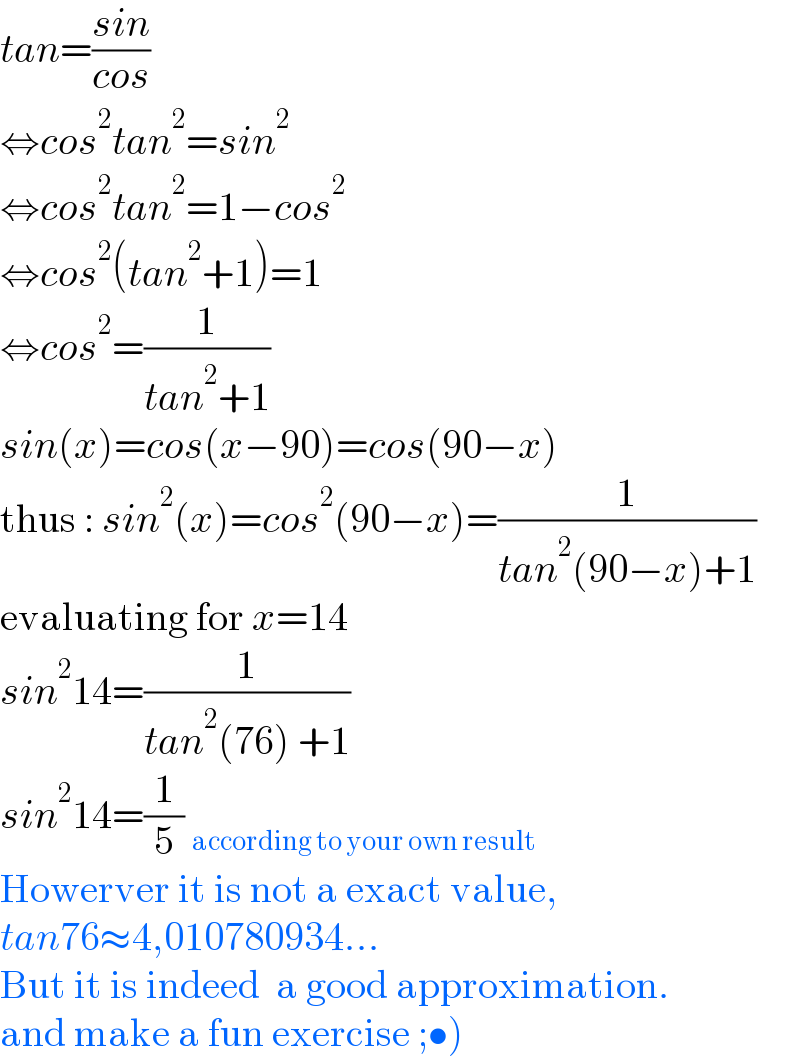
$${tan}=\frac{{sin}}{{cos}} \\ $$$$\Leftrightarrow{cos}^{\mathrm{2}} {tan}^{\mathrm{2}} ={sin}^{\mathrm{2}} \\ $$$$\Leftrightarrow{cos}^{\mathrm{2}} {tan}^{\mathrm{2}} =\mathrm{1}−{cos}^{\mathrm{2}} \\ $$$$\Leftrightarrow{cos}^{\mathrm{2}} \left({tan}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{1} \\ $$$$\Leftrightarrow{cos}^{\mathrm{2}} =\frac{\mathrm{1}}{{tan}^{\mathrm{2}} +\mathrm{1}} \\ $$$${sin}\left({x}\right)={cos}\left({x}−\mathrm{90}\right)={cos}\left(\mathrm{90}−{x}\right) \\ $$$$\mathrm{thus}\::\:{sin}^{\mathrm{2}} \left({x}\right)={cos}^{\mathrm{2}} \left(\mathrm{90}−{x}\right)=\frac{\mathrm{1}}{{tan}^{\mathrm{2}} \left(\mathrm{90}−{x}\right)+\mathrm{1}} \\ $$$$\mathrm{evaluating}\:\mathrm{for}\:{x}=\mathrm{14} \\ $$$${sin}^{\mathrm{2}} \mathrm{14}=\frac{\mathrm{1}}{{tan}^{\mathrm{2}} \left(\mathrm{76}\right)\:+\mathrm{1}} \\ $$$${sin}^{\mathrm{2}} \mathrm{14}=\frac{\mathrm{1}}{\mathrm{5}}\:_{\mathrm{according}\:\mathrm{to}\:\mathrm{your}\:\mathrm{own}\:\mathrm{result}} \\ $$$$\mathrm{Howerver}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{exact}\:\mathrm{value}, \\ $$$${tan}\mathrm{76}\approx\mathrm{4},\mathrm{010780934}… \\ $$$$\mathrm{But}\:\mathrm{it}\:\mathrm{is}\:\mathrm{indeed}\:\:\mathrm{a}\:\mathrm{good}\:\mathrm{approximation}. \\ $$$$\left.\mathrm{and}\:\mathrm{make}\:\mathrm{a}\:\mathrm{fun}\:\mathrm{exercise}\:;\bullet\right) \\ $$
