Question Number 11822 by Joel576 last updated on 01/Apr/17

$$\int\:\frac{\mathrm{tan}\:{x}}{\mathrm{1}\:+\:\mathrm{sin}\:{x}}\:{dx} \\ $$
Answered by ajfour last updated on 01/Apr/17
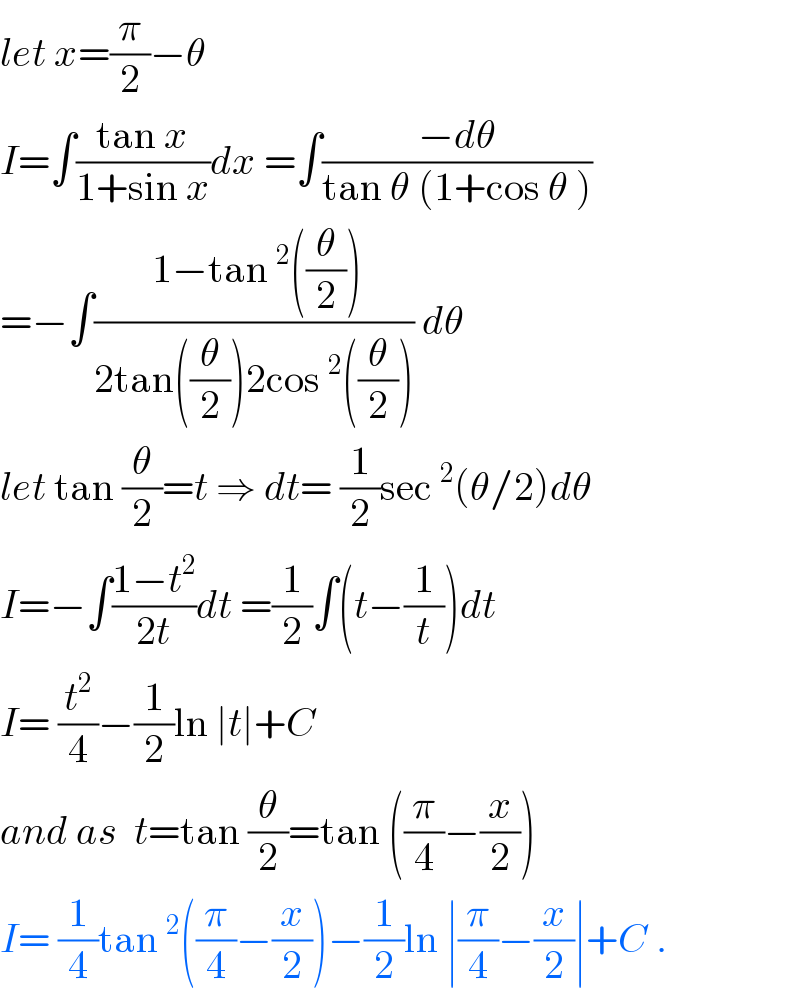
$${let}\:{x}=\frac{\pi}{\mathrm{2}}−\theta \\ $$$${I}=\int\frac{\mathrm{tan}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}\:=\int\frac{−{d}\theta}{\mathrm{tan}\:\theta\:\left(\mathrm{1}+\mathrm{cos}\:\theta\:\right)} \\ $$$$=−\int\frac{\:\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2tan}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}\:{d}\theta \\ $$$${let}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={t}\:\Rightarrow\:{dt}=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \left(\theta/\mathrm{2}\right){d}\theta \\ $$$${I}=−\int\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}{t}}{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left({t}−\frac{\mathrm{1}}{{t}}\right){dt} \\ $$$${I}=\:\frac{{t}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{t}\mid+{C} \\ $$$${and}\:{as}\:\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right) \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\mid+{C}\:. \\ $$
Commented by Joel576 last updated on 02/Apr/17

$${thank}\:{you}\:{very}\:{much} \\ $$
