Question Number 702 by 123456 last updated on 01/Mar/15

$$\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x}+\mathrm{tan}\:\mathrm{4}{x}+\centerdot\centerdot\centerdot+\mathrm{tan}\:\mathrm{2}^{{n}} {x}=? \\ $$
Commented by prakash jain last updated on 01/Mar/15

$$\mathrm{Do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{a}\:\mathrm{closed}\:\mathrm{form}\:\mathrm{expression}? \\ $$
Commented by prakash jain last updated on 02/Mar/15
![Did you mean? tan x+2tan 2x+2^2 tan 4x+...+2^n tan 2^n x= −2^(n+1) cosec 2^(n+1) x sin x∙[cos 2^(n+1) x cosec x−(1/2^(n+1) )sin 2^(n+1) x cosec x cot x]](https://www.tinkutara.com/question/Q708.png)
$$\mathrm{Did}\:\mathrm{you}\:\mathrm{mean}? \\ $$$$\mathrm{tan}\:{x}+\mathrm{2tan}\:\mathrm{2}{x}+\mathrm{2}^{\mathrm{2}} \mathrm{tan}\:\mathrm{4}{x}+…+\mathrm{2}^{{n}} \mathrm{tan}\:\mathrm{2}^{{n}} {x}= \\ $$$$−\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cosec}\:\mathrm{2}^{{n}+\mathrm{1}} {x}\:\mathrm{sin}\:{x}\centerdot\left[\mathrm{cos}\:\mathrm{2}^{\mathrm{n}+\mathrm{1}} {x}\:\mathrm{cosec}\:{x}−\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\mathrm{sin}\:\mathrm{2}^{{n}+\mathrm{1}} {x}\:\mathrm{cosec}\:{x}\:\mathrm{cot}\:{x}\right] \\ $$
Commented by 123456 last updated on 07/Apr/15
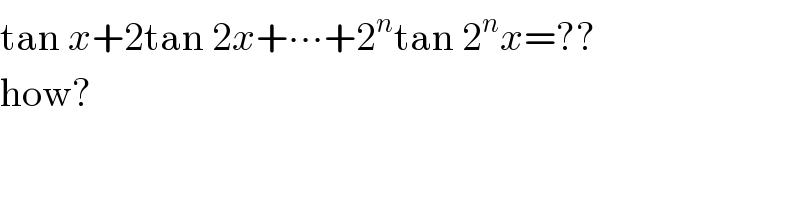
$$\mathrm{tan}\:{x}+\mathrm{2tan}\:\mathrm{2}{x}+\centerdot\centerdot\centerdot+\mathrm{2}^{{n}} \mathrm{tan}\:\mathrm{2}^{{n}} {x}=?? \\ $$$$\mathrm{how}? \\ $$
