Question Number 9414 by Rohit kumar last updated on 06/Dec/16
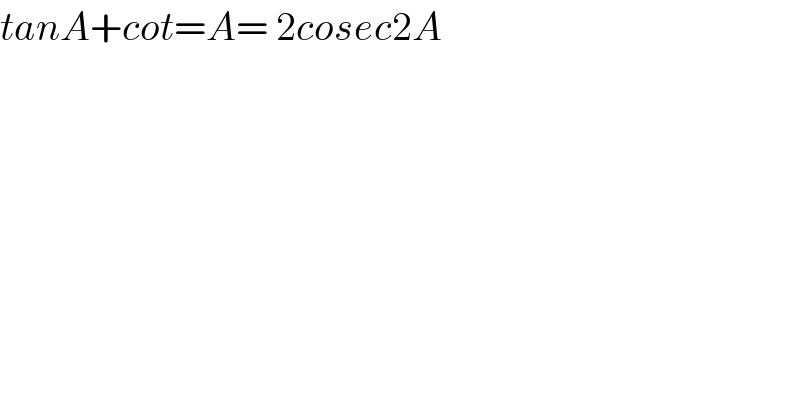
$${tanA}+{cot}={A}=\:\mathrm{2}{cosec}\mathrm{2}{A} \\ $$
Answered by ridwan balatif last updated on 06/Dec/16
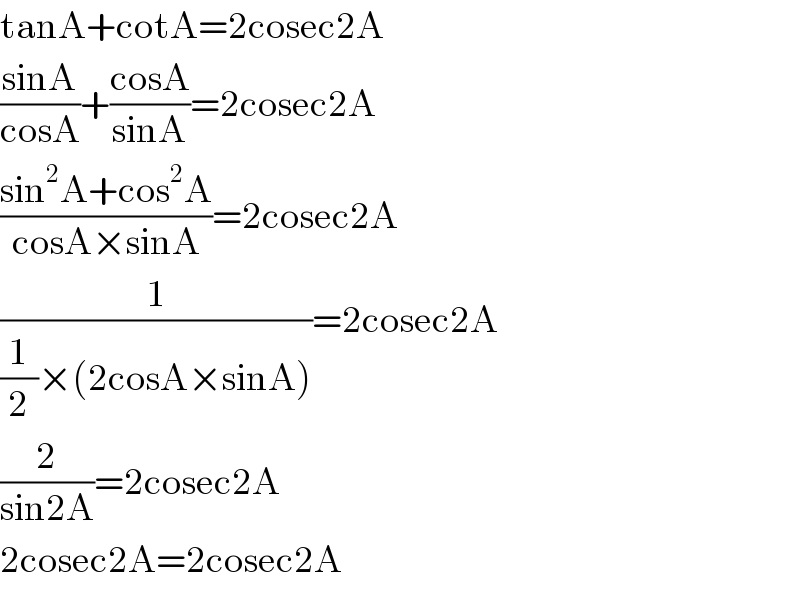
$$\mathrm{tanA}+\mathrm{cotA}=\mathrm{2cosec2A} \\ $$$$\frac{\mathrm{sinA}}{\mathrm{cosA}}+\frac{\mathrm{cosA}}{\mathrm{sinA}}=\mathrm{2cosec2A} \\ $$$$\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{cos}^{\mathrm{2}} \mathrm{A}}{\mathrm{cosA}×\mathrm{sinA}}=\mathrm{2cosec2A} \\ $$$$\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{2cosA}×\mathrm{sinA}\right)}=\mathrm{2cosec2A} \\ $$$$\frac{\mathrm{2}}{\mathrm{sin2A}}=\mathrm{2cosec2A} \\ $$$$\mathrm{2cosec2A}=\mathrm{2cosec2A} \\ $$
