Menu Close

tanf-df-dx-f-

Tinku Tara 0 Comments
Pin




Question Number 3763 by 123456 last updated on 19/Dec/15
tanf=(df/dx) f=?
$$\mathrm{tan}{f}=\frac{{df}}{{dx}} \\ $$$${f}=? \\ $$
Commented by Filup last updated on 19/Dec/15
(df/dx)=tan f ∫secf df=x+c
$$\frac{{df}}{{dx}}=\mathrm{tan}\:{f} \\ $$$$\int\mathrm{sec}{f}\:{df}={x}+{c} \\ $$
Answered by Yozzii last updated on 20/Dec/15
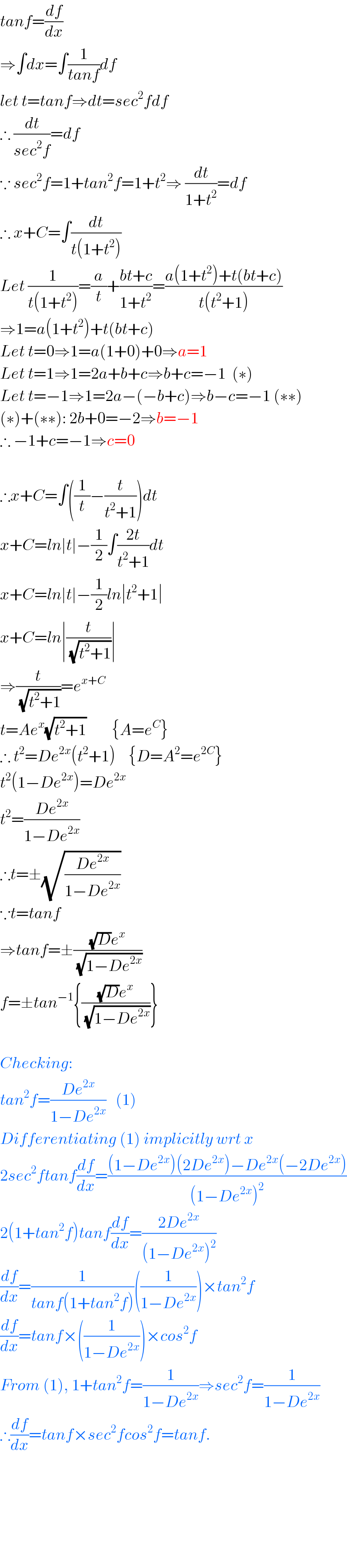
tanf=(df/dx) ⇒∫dx=∫(1/(tanf))df let t=tanf⇒dt=sec^2 fdf ∴ (dt/(sec^2 f))=df ∵ sec^2 f=1+tan^2 f=1+t^2 ⇒ (dt/(1+t^2 ))=df ∴ x+C=∫(dt/(t(1+t^2 ))) Let (1/(t(1+t^2 )))=(a/t)+((bt+c)/(1+t^2 ))=((a(1+t^2 )+t(bt+c))/(t(t^2 +1))) ⇒1=a(1+t^2 )+t(bt+c) Let t=0⇒1=a(1+0)+0⇒a=1 Let t=1⇒1=2a+b+c⇒b+c=−1 (∗) Let t=−1⇒1=2a−(−b+c)⇒b−c=−1 (∗∗) (∗)+(∗∗): 2b+0=−2⇒b=−1 ∴ −1+c=−1⇒c=0 ∴x+C=∫((1/t)−(t/(t^2 +1)))dt x+C=ln∣t∣−(1/2)∫((2t)/(t^2 +1))dt x+C=ln∣t∣−(1/2)ln∣t^2 +1∣ x+C=ln∣(t/( (√(t^2 +1))))∣ ⇒(t/( (√(t^2 +1))))=e^(x+C) t=Ae^x (√(t^2 +1)) {A=e^C } ∴ t^2 =De^(2x) (t^2 +1) {D=A^2 =e^(2C) } t^2 (1−De^(2x) )=De^(2x) t^2 =((De^(2x) )/(1−De^(2x) )) ∴t=±(√((De^(2x) )/(1−De^(2x) ))) ∵t=tanf ⇒tanf=±(((√D)e^x )/( (√(1−De^(2x) )))) f=±tan^(−1) {(((√D)e^x )/( (√(1−De^(2x) ))))} Checking: tan^2 f=((De^(2x) )/(1−De^(2x) )) (1) Differentiating (1) implicitly wrt x 2sec^2 ftanf(df/dx)=(((1−De^(2x) )(2De^(2x) )−De^(2x) (−2De^(2x) ))/((1−De^(2x) )^2 )) 2(1+tan^2 f)tanf(df/dx)=((2De^(2x) )/((1−De^(2x) )^2 )) (df/dx)=(1/(tanf(1+tan^2 f)))((1/(1−De^(2x) )))×tan^2 f (df/dx)=tanf×((1/(1−De^(2x) )))×cos^2 f From (1), 1+tan^2 f=(1/(1−De^(2x) ))⇒sec^2 f=(1/(1−De^(2x) )) ∴(df/dx)=tanf×sec^2 fcos^2 f=tanf.
$${tanf}=\frac{{df}}{{dx}} \\ $$$$\Rightarrow\int{dx}=\int\frac{\mathrm{1}}{{tanf}}{df} \\ $$$${let}\:{t}={tanf}\Rightarrow{dt}={sec}^{\mathrm{2}} {fdf} \\ $$$$\therefore\:\frac{{dt}}{{sec}^{\mathrm{2}} {f}}={df} \\ $$$$\because\:{sec}^{\mathrm{2}} {f}=\mathrm{1}+{tan}^{\mathrm{2}} {f}=\mathrm{1}+{t}^{\mathrm{2}} \Rightarrow\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }={df} \\ $$$$\therefore\:{x}+{C}=\int\frac{{dt}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$${Let}\:\frac{\mathrm{1}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}=\frac{{a}}{{t}}+\frac{{bt}+{c}}{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{{a}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+{t}\left({bt}+{c}\right)}{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{1}={a}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+{t}\left({bt}+{c}\right) \\ $$$${Let}\:{t}=\mathrm{0}\Rightarrow\mathrm{1}={a}\left(\mathrm{1}+\mathrm{0}\right)+\mathrm{0}\Rightarrow{a}=\mathrm{1} \\ $$$${Let}\:{t}=\mathrm{1}\Rightarrow\mathrm{1}=\mathrm{2}{a}+{b}+{c}\Rightarrow{b}+{c}=−\mathrm{1}\:\:\left(\ast\right) \\ $$$${Let}\:{t}=−\mathrm{1}\Rightarrow\mathrm{1}=\mathrm{2}{a}−\left(−{b}+{c}\right)\Rightarrow{b}−{c}=−\mathrm{1}\:\left(\ast\ast\right) \\ $$$$\left(\ast\right)+\left(\ast\ast\right):\:\mathrm{2}{b}+\mathrm{0}=−\mathrm{2}\Rightarrow{b}=−\mathrm{1} \\ $$$$\therefore\:−\mathrm{1}+{c}=−\mathrm{1}\Rightarrow{c}=\mathrm{0} \\ $$$$ \\ $$$$\therefore{x}+{C}=\int\left(\frac{\mathrm{1}}{{t}}−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt} \\ $$$${x}+{C}={ln}\mid{t}\mid−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$${x}+{C}={ln}\mid{t}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{t}^{\mathrm{2}} +\mathrm{1}\mid \\ $$$${x}+{C}={ln}\mid\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\mid \\ $$$$\Rightarrow\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}={e}^{{x}+{C}} \\ $$$${t}={Ae}^{{x}} \sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:\:\:\:\:\:\:\:\left\{{A}={e}^{{C}} \right\} \\ $$$$\therefore\:{t}^{\mathrm{2}} ={De}^{\mathrm{2}{x}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)\:\:\:\:\left\{{D}={A}^{\mathrm{2}} ={e}^{\mathrm{2}{C}} \right\} \\ $$$${t}^{\mathrm{2}} \left(\mathrm{1}−{De}^{\mathrm{2}{x}} \right)={De}^{\mathrm{2}{x}} \\ $$$${t}^{\mathrm{2}} =\frac{{De}^{\mathrm{2}{x}} }{\mathrm{1}−{De}^{\mathrm{2}{x}} } \\ $$$$\therefore{t}=\pm\sqrt{\frac{{De}^{\mathrm{2}{x}} }{\mathrm{1}−{De}^{\mathrm{2}{x}} }} \\ $$$$\because{t}={tanf} \\ $$$$\Rightarrow{tanf}=\pm\frac{\sqrt{{D}}{e}^{{x}} }{\:\sqrt{\mathrm{1}−{De}^{\mathrm{2}{x}} }} \\ $$$${f}=\pm{tan}^{−\mathrm{1}} \left\{\frac{\sqrt{{D}}{e}^{{x}} }{\:\sqrt{\mathrm{1}−{De}^{\mathrm{2}{x}} }}\right\} \\ $$$$ \\ $$$${Checking}: \\ $$$${tan}^{\mathrm{2}} {f}=\frac{{De}^{\mathrm{2}{x}} }{\mathrm{1}−{De}^{\mathrm{2}{x}} }\:\:\:\left(\mathrm{1}\right) \\ $$$${Differentiating}\:\left(\mathrm{1}\right)\:{implicitly}\:{wrt}\:{x}\: \\ $$$$\mathrm{2}{sec}^{\mathrm{2}} {ftanf}\frac{{df}}{{dx}}=\frac{\left(\mathrm{1}−{De}^{\mathrm{2}{x}} \right)\left(\mathrm{2}{De}^{\mathrm{2}{x}} \right)−{De}^{\mathrm{2}{x}} \left(−\mathrm{2}{De}^{\mathrm{2}{x}} \right)}{\left(\mathrm{1}−{De}^{\mathrm{2}{x}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {f}\right){tanf}\frac{{df}}{{dx}}=\frac{\mathrm{2}{De}^{\mathrm{2}{x}} }{\left(\mathrm{1}−{De}^{\mathrm{2}{x}} \right)^{\mathrm{2}} } \\ $$$$\frac{{df}}{{dx}}=\frac{\mathrm{1}}{{tanf}\left(\mathrm{1}+{tan}^{\mathrm{2}} {f}\right)}\left(\frac{\mathrm{1}}{\mathrm{1}−{De}^{\mathrm{2}{x}} }\right)×{tan}^{\mathrm{2}} {f} \\ $$$$\frac{{df}}{{dx}}={tanf}×\left(\frac{\mathrm{1}}{\mathrm{1}−{De}^{\mathrm{2}{x}} }\right)×{cos}^{\mathrm{2}} {f} \\ $$$${From}\:\left(\mathrm{1}\right),\:\mathrm{1}+{tan}^{\mathrm{2}} {f}=\frac{\mathrm{1}}{\mathrm{1}−{De}^{\mathrm{2}{x}} }\Rightarrow{sec}^{\mathrm{2}} {f}=\frac{\mathrm{1}}{\mathrm{1}−{De}^{\mathrm{2}{x}} } \\ $$$$\therefore\frac{{df}}{{dx}}={tanf}×{sec}^{\mathrm{2}} {fcos}^{\mathrm{2}} {f}={tanf}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *