Question Number 11172 by agni5 last updated on 15/Mar/17
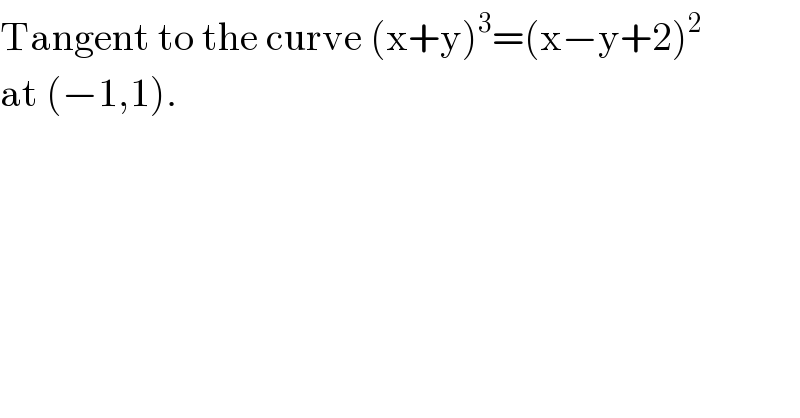
$$\mathrm{Tangent}\:\mathrm{to}\:\mathrm{the}\:\mathrm{curve}\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{3}} =\left(\mathrm{x}−\mathrm{y}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{at}\:\left(−\mathrm{1},\mathrm{1}\right). \\ $$
Answered by ajfour last updated on 15/Mar/17

$${y}={x}+\mathrm{2} \\ $$
Commented by ajfour last updated on 15/Mar/17

Commented by ajfour last updated on 15/Mar/17
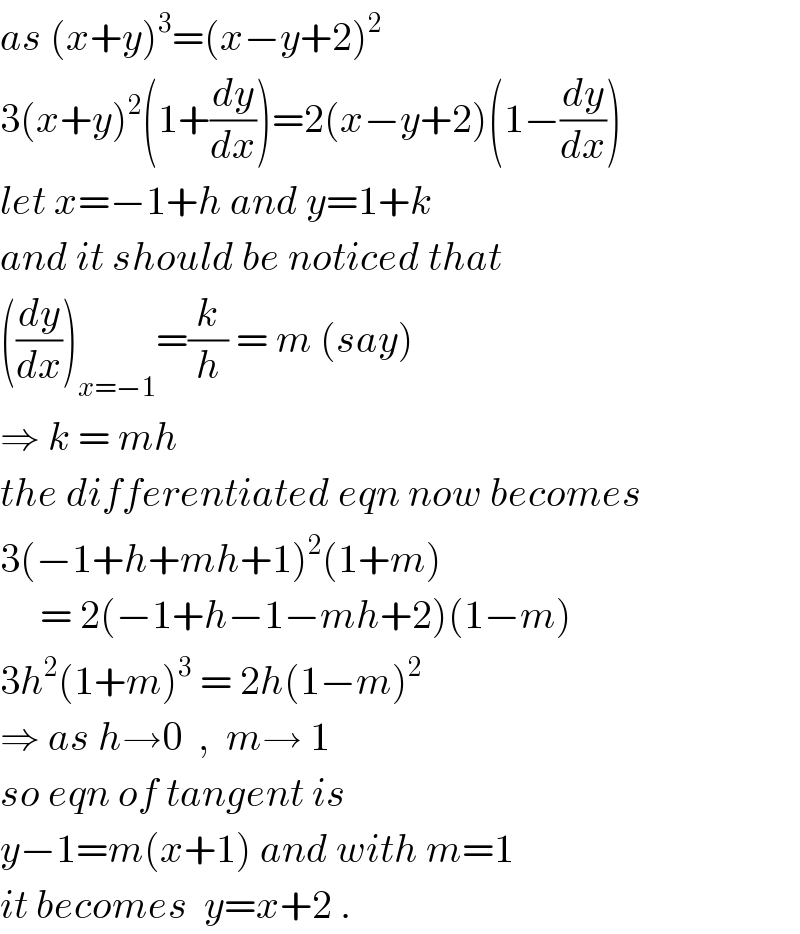
$${as}\:\left({x}+{y}\right)^{\mathrm{3}} =\left({x}−{y}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}\left({x}+{y}\right)^{\mathrm{2}} \left(\mathrm{1}+\frac{{dy}}{{dx}}\right)=\mathrm{2}\left({x}−{y}+\mathrm{2}\right)\left(\mathrm{1}−\frac{{dy}}{{dx}}\right) \\ $$$${let}\:{x}=−\mathrm{1}+{h}\:{and}\:{y}=\mathrm{1}+{k} \\ $$$${and}\:{it}\:{should}\:{be}\:{noticed}\:{that} \\ $$$$\left(\frac{{dy}}{{dx}}\right)_{{x}=−\mathrm{1}} =\frac{{k}}{{h}}\:=\:{m}\:\left({say}\right) \\ $$$$\Rightarrow\:{k}\:=\:{mh} \\ $$$${the}\:{differentiated}\:{eqn}\:{now}\:{becomes} \\ $$$$\mathrm{3}\left(−\mathrm{1}+{h}+{mh}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+{m}\right) \\ $$$$\:\:\:\:\:=\:\mathrm{2}\left(−\mathrm{1}+{h}−\mathrm{1}−{mh}+\mathrm{2}\right)\left(\mathrm{1}−{m}\right) \\ $$$$\mathrm{3}{h}^{\mathrm{2}} \left(\mathrm{1}+{m}\right)^{\mathrm{3}} \:=\:\mathrm{2}{h}\left(\mathrm{1}−{m}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{as}\:{h}\rightarrow\mathrm{0}\:\:,\:\:{m}\rightarrow\:\mathrm{1} \\ $$$${so}\:{eqn}\:{of}\:{tangent}\:{is} \\ $$$${y}−\mathrm{1}={m}\left({x}+\mathrm{1}\right)\:{and}\:{with}\:{m}=\mathrm{1} \\ $$$${it}\:{becomes}\:\:{y}={x}+\mathrm{2}\:. \\ $$
