Question Number 75847 by behi83417@gmail.com last updated on 18/Dec/19
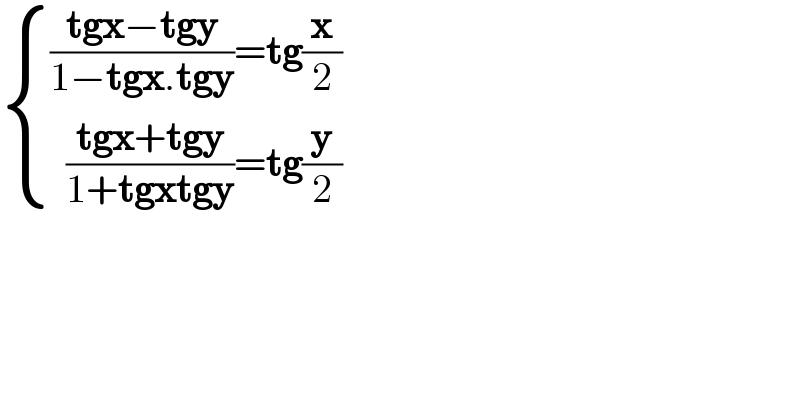
$$\begin{cases}{\frac{\boldsymbol{\mathrm{tgx}}−\boldsymbol{\mathrm{tgy}}}{\mathrm{1}−\boldsymbol{\mathrm{tgx}}.\boldsymbol{\mathrm{tgy}}}=\boldsymbol{\mathrm{tg}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}}\\{\:\:\frac{\boldsymbol{\mathrm{tgx}}+\boldsymbol{\mathrm{tgy}}}{\mathrm{1}+\boldsymbol{\mathrm{tgxtgy}}}=\boldsymbol{\mathrm{tg}}\frac{\boldsymbol{\mathrm{y}}}{\mathrm{2}}}\end{cases} \\ $$
Commented by MJS last updated on 19/Dec/19

$$\mathrm{the}\:\mathrm{path}\:\mathrm{is} \\ $$$$\mathrm{let}\:{x}=\mathrm{2arctan}\:{p};\:{y}=\mathrm{2arctan}\:{q} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{u}^{\mathrm{3}} {v}^{\mathrm{2}} −{u}^{\mathrm{3}} −\mathrm{6}{u}^{\mathrm{2}} {v}+{uv}^{\mathrm{2}} −{u}+\mathrm{2}{v}=\mathrm{0}}\\{{u}^{\mathrm{2}} {v}^{\mathrm{3}} +{u}^{\mathrm{2}} {v}+\mathrm{6}{uv}^{\mathrm{2}} −{v}^{\mathrm{3}} −\mathrm{2}{u}−{v}=\mathrm{0}}\end{cases} \\ $$$$\mathrm{solve}\:\mathrm{the}\:\mathrm{first}\:\mathrm{one}\:\mathrm{for}\:{v}\:\mathrm{and}\:\mathrm{insert}\:\mathrm{into}\:\mathrm{the} \\ $$$$\mathrm{second}\:\mathrm{one} \\ $$$$\Rightarrow\:\mathrm{degree}\:\mathrm{9}\:\mathrm{for}\:{u}^{\mathrm{2}} \:\mathrm{with}\:\mathrm{triple}\:\mathrm{solution}\:{u}^{\mathrm{2}} =−\mathrm{1}\: \\ $$$$\Rightarrow\:\mathrm{degree}\:\mathrm{6}\:\mathrm{for}\:{u}^{\mathrm{2}} ,\:\mathrm{solve}\:\mathrm{approximately}\:\mathrm{and} \\ $$$$\mathrm{test}\:\mathrm{all}\:\mathrm{solutions} \\ $$$$\Rightarrow \\ $$$$\mathrm{0}\leqslant{x},\:{y}<\mathrm{2}\pi \\ $$$${x}_{\mathrm{1}} \approx\mathrm{4}.\mathrm{94542}\wedge{y}_{\mathrm{1}} \approx.\mathrm{973062} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{1}.\mathrm{33776}\wedge{y}_{\mathrm{2}} \approx\mathrm{5}.\mathrm{31012} \\ $$$${x}_{\mathrm{3}} ={y}_{\mathrm{2}} \wedge{y}_{\mathrm{3}} ={x}_{\mathrm{1}} \\ $$$${x}_{\mathrm{4}} ={y}_{\mathrm{1}} \wedge{y}_{\mathrm{4}} ={x}_{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 19/Dec/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{proph}:\mathrm{MJS}. \\ $$$$\mathrm{you}\:\mathrm{are}\:\mathrm{the}\:\mathrm{best}.\mathrm{thank}\:\mathrm{god}\:\mathrm{for}\:\mathrm{being}\:\mathrm{you} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{forum}. \\ $$
