Question Number 1777 by 112358 last updated on 22/Sep/15
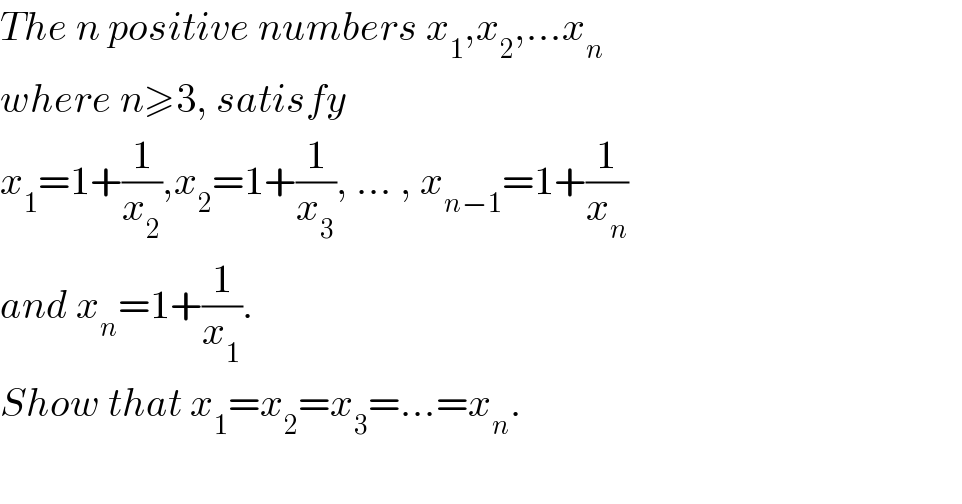
$${The}\:{n}\:{positive}\:{numbers}\:{x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,…{x}_{{n}} \\ $$$${where}\:{n}\geqslant\mathrm{3},\:{satisfy}\: \\ $$$${x}_{\mathrm{1}} =\mathrm{1}+\frac{\mathrm{1}}{{x}_{\mathrm{2}} },{x}_{\mathrm{2}} =\mathrm{1}+\frac{\mathrm{1}}{{x}_{\mathrm{3}} },\:…\:,\:{x}_{{n}−\mathrm{1}} =\mathrm{1}+\frac{\mathrm{1}}{{x}_{{n}} } \\ $$$${and}\:{x}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{{x}_{\mathrm{1}} }.\: \\ $$$${Show}\:{that}\:{x}_{\mathrm{1}} ={x}_{\mathrm{2}} ={x}_{\mathrm{3}} =…={x}_{{n}} . \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 26/Sep/15

$${This}\:\:{problem}\:{can}\:{be}\:{translated}\:{in}\:{modulo}\:{form}\: \\ $$$${as}\:{follows}: \\ $$$$\:\:\:\:\:\:\:\:\:''\:{The}\:{n}\:{positive}\:{numbers}\:{x}_{\mathrm{0}} ,\:{x}_{\mathrm{1}} ,…,{x}_{{n}−\mathrm{1}} \\ $$$${where}\:{n}\geqslant\mathrm{3},\:{satisfy}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{x}_{{i}\:\:\left({mod}\:{n}\right)} =\mathrm{1}+\frac{\mathrm{1}}{{x}_{\left({i}\:+\mathrm{1}\right)\:\left({mod}\:{n}\right)} }\:\:\:\:\:\:,\:{i}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…\right\}\: \\ $$$${Show}\:{that} \\ $$$$\:\:\:\:\:\:{x}_{\mathrm{0}} ={x}_{\mathrm{1}} ={x}_{\mathrm{2}} =…={x}_{{n}−\mathrm{2}} ={x}_{{n}−\mathrm{1}} \:\:\:\:'' \\ $$$${Let}\:{the}\:{above}\:{statment}\:{be}\:{denoted}\:{by}\:{P}\left({n}\right). \\ $$$${Then}\:{by}\:{mathematical}\:{induction} \\ $$$$\left(\mathrm{1}\right)\:{P}\left({n}\right)\:{should}\:{be}\:{proved}\:{for}\:{n}=\mathrm{3}. \\ $$$$\left(\mathrm{2}\right)\:{P}\left({k}\right)\:{is}\:{supposed}\:{to}\:{be}\:{true}\:{and}\:{P}\left({k}+\mathrm{1}\right)\:{should}\:{be} \\ $$$${proved}\:\:{true}. \\ $$$$\left(\mathrm{1}\right)\:{is}\:{easy}\:{but}\:\left(\mathrm{2}\right)\:{is}\:{challenging}. \\ $$
