Question Number 138999 by bramlexs22 last updated on 21/Apr/21

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions} \\ $$$$\mathrm{of}\:\mathrm{equations}\:\sqrt{\mathrm{13}−\mathrm{18tan}\:\mathrm{x}}\:=\:\mathrm{6tan}\:\mathrm{x}−\mathrm{3} \\ $$$$\mathrm{where}\:−\mathrm{2}\pi<\mathrm{x}<\mathrm{2}\pi\:\mathrm{is} \\ $$
Answered by EDWIN88 last updated on 21/Apr/21
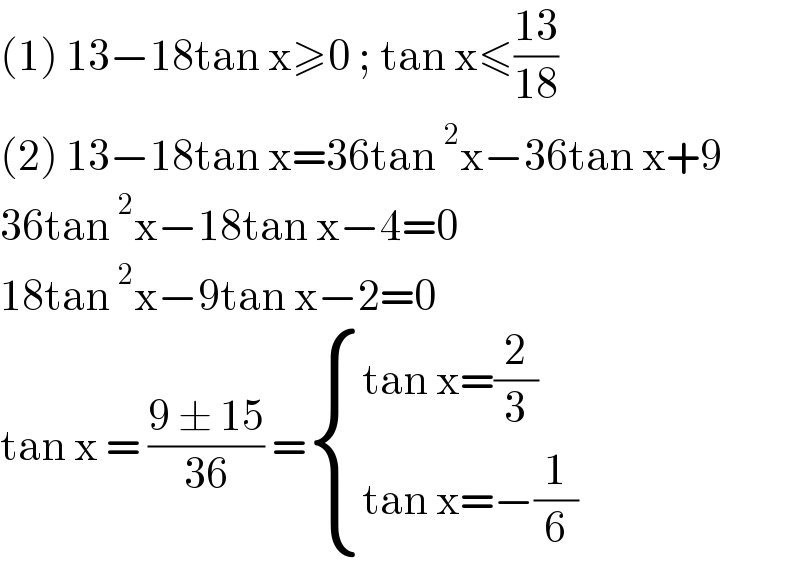
$$\left(\mathrm{1}\right)\:\mathrm{13}−\mathrm{18tan}\:\mathrm{x}\geqslant\mathrm{0}\:;\:\mathrm{tan}\:\mathrm{x}\leqslant\frac{\mathrm{13}}{\mathrm{18}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{13}−\mathrm{18tan}\:\mathrm{x}=\mathrm{36tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{36tan}\:\mathrm{x}+\mathrm{9} \\ $$$$\mathrm{36tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{18tan}\:\mathrm{x}−\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{18tan}\:^{\mathrm{2}} \mathrm{x}−\mathrm{9tan}\:\mathrm{x}−\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{tan}\:\mathrm{x}\:=\:\frac{\mathrm{9}\:\pm\:\mathrm{15}}{\mathrm{36}}\:=\begin{cases}{\mathrm{tan}\:\mathrm{x}=\frac{\mathrm{2}}{\mathrm{3}}}\\{\mathrm{tan}\:\mathrm{x}=−\frac{\mathrm{1}}{\mathrm{6}}}\end{cases} \\ $$
