Question Number 136293 by mr W last updated on 20/Mar/21
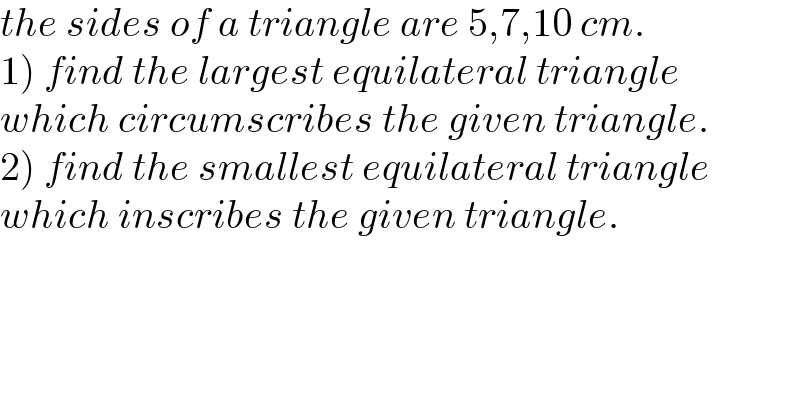
$${the}\:{sides}\:{of}\:{a}\:{triangle}\:{are}\:\mathrm{5},\mathrm{7},\mathrm{10}\:{cm}. \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{largest}\:{equilateral}\:{triangle} \\ $$$${which}\:{circumscribes}\:{the}\:{given}\:{triangle}. \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{smallest}\:{equilateral}\:{triangle} \\ $$$${which}\:{inscribes}\:{the}\:{given}\:{triangle}. \\ $$
Commented by mr W last updated on 20/Mar/21
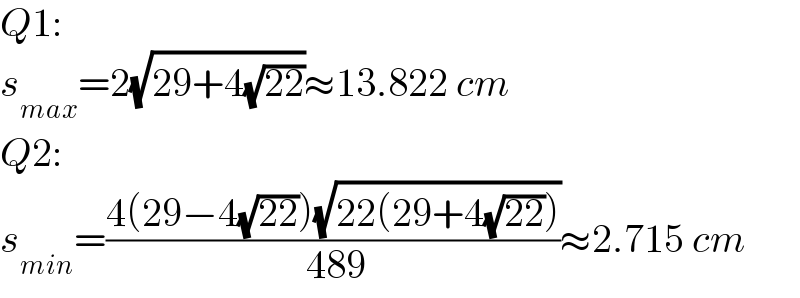
$${Q}\mathrm{1}: \\ $$$${s}_{{max}} =\mathrm{2}\sqrt{\mathrm{29}+\mathrm{4}\sqrt{\mathrm{22}}}\approx\mathrm{13}.\mathrm{822}\:{cm} \\ $$$${Q}\mathrm{2}: \\ $$$${s}_{{min}} =\frac{\mathrm{4}\left(\mathrm{29}−\mathrm{4}\sqrt{\mathrm{22}}\right)\sqrt{\mathrm{22}\left(\mathrm{29}+\mathrm{4}\sqrt{\mathrm{22}}\right)}}{\:\mathrm{489}}\approx\mathrm{2}.\mathrm{715}\:{cm} \\ $$
