Menu Close

The-solution-set-of-equation-cos-2-x-cos-2-2x-cos-2-3x-1-on-0-x-2pi-

Tinku Tara 0 Comments
Pin




Question Number 137382 by bramlexs22 last updated on 02/Apr/21
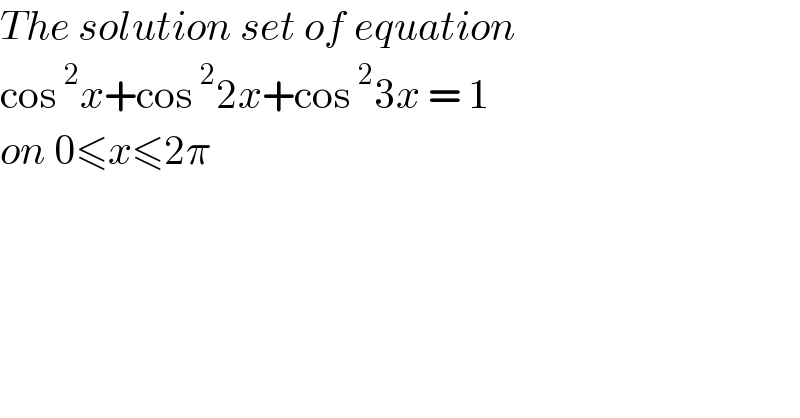
The solution set of equation cos^2 x+cos^2 2x+cos^2 3x = 1 on 0≤x≤2π
$${The}\:{solution}\:{set}\:{of}\:{equation} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{x}\:=\:\mathrm{1}\: \\ $$$${on}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{2}\pi \\ $$
Commented by MJS_new last updated on 03/Apr/21
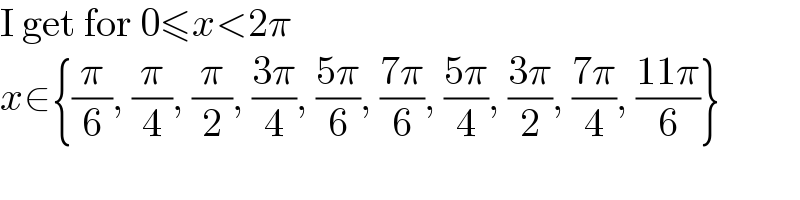
I get for 0≤x<2π x∈{(π/6), (π/4), (π/2), ((3π)/4), ((5π)/6), ((7π)/6), ((5π)/4), ((3π)/2), ((7π)/4), ((11π)/6)}
$$\mathrm{I}\:\mathrm{get}\:\mathrm{for}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi \\ $$$${x}\in\left\{\frac{\pi}{\mathrm{6}},\:\frac{\pi}{\mathrm{4}},\:\frac{\pi}{\mathrm{2}},\:\frac{\mathrm{3}\pi}{\mathrm{4}},\:\frac{\mathrm{5}\pi}{\mathrm{6}},\:\frac{\mathrm{7}\pi}{\mathrm{6}},\:\frac{\mathrm{5}\pi}{\mathrm{4}},\:\frac{\mathrm{3}\pi}{\mathrm{2}},\:\frac{\mathrm{7}\pi}{\mathrm{4}},\:\frac{\mathrm{11}\pi}{\mathrm{6}}\right\} \\ $$
Answered by EDWIN88 last updated on 02/Apr/21
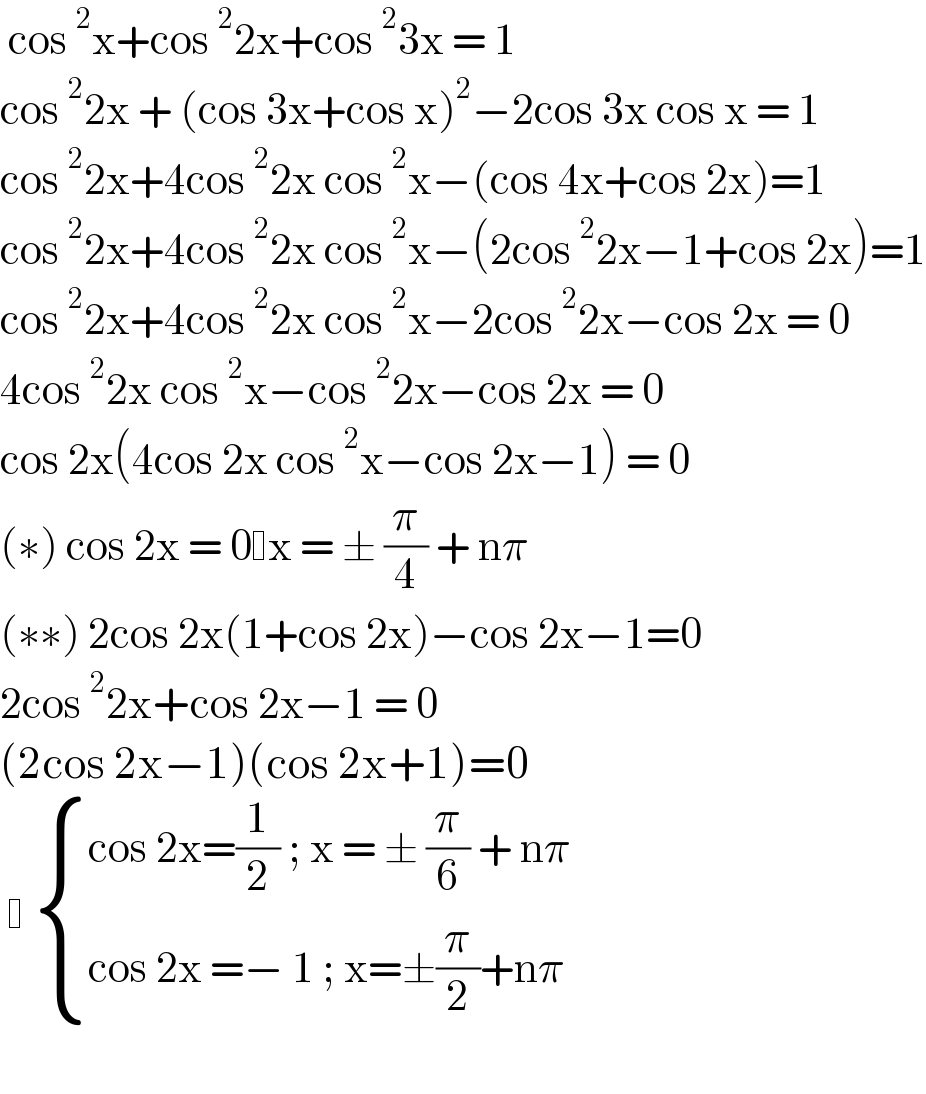
cos^2 x+cos^2 2x+cos^2 3x = 1 cos^2 2x + (cos 3x+cos x)^2 −2cos 3x cos x = 1 cos^2 2x+4cos^2 2x cos^2 x−(cos 4x+cos 2x)=1 cos^2 2x+4cos^2 2x cos^2 x−(2cos^2 2x−1+cos 2x)=1 cos^2 2x+4cos^2 2x cos^2 x−2cos^2 2x−cos 2x = 0 4cos^2 2x cos^2 x−cos^2 2x−cos 2x = 0 cos 2x(4cos 2x cos^2 x−cos 2x−1) = 0 (∗) cos 2x = 0 x = ± (π/4) + nπ (∗∗) 2cos 2x(1+cos 2x)−cos 2x−1=0 2cos^2 2x+cos 2x−1 = 0 (2cos 2x−1)(cos 2x+1)=0 { ((cos 2x=(1/2) ; x = ± (π/6) + nπ)),((cos 2x =− 1 ; x=±(π/2)+nπ )) :}
$$\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{3x}\:=\:\mathrm{1} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}\:+\:\left(\mathrm{cos}\:\mathrm{3x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} −\mathrm{2cos}\:\mathrm{3x}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{1} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{4cos}\:^{\mathrm{2}} \mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\left(\mathrm{cos}\:\mathrm{4x}+\mathrm{cos}\:\mathrm{2x}\right)=\mathrm{1} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{4cos}\:^{\mathrm{2}} \mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\left(\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2x}−\mathrm{1}+\mathrm{cos}\:\mathrm{2x}\right)=\mathrm{1} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{4cos}\:^{\mathrm{2}} \mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2x}−\mathrm{cos}\:\mathrm{2x}\:=\:\mathrm{0} \\ $$$$\mathrm{4cos}\:^{\mathrm{2}} \mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}−\mathrm{cos}\:\mathrm{2x}\:=\:\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{2x}\left(\mathrm{4cos}\:\mathrm{2x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}\:\mathrm{2x}−\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\left(\ast\right)\:\mathrm{cos}\:\mathrm{2x}\:=\:\mathrm{0} \mathrm{x}\:=\:\pm\:\frac{\pi}{\mathrm{4}}\:+\:\mathrm{n}\pi \\ $$$$\left(\ast\ast\right)\:\mathrm{2cos}\:\mathrm{2x}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2x}\right)−\mathrm{cos}\:\mathrm{2x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2x}+\mathrm{cos}\:\mathrm{2x}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{2cos}\:\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{cos}\:\mathrm{2x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\: \:\begin{cases}{\mathrm{cos}\:\mathrm{2x}=\frac{\mathrm{1}}{\mathrm{2}}\:;\:\mathrm{x}\:=\:\pm\:\frac{\pi}{\mathrm{6}}\:+\:\mathrm{n}\pi}\\{\mathrm{cos}\:\mathrm{2x}\:=−\:\mathrm{1}\:;\:\mathrm{x}=\pm\frac{\pi}{\mathrm{2}}+\mathrm{n}\pi\:}\end{cases} \\ $$$$ \\ $$
Answered by liberty last updated on 02/Apr/21
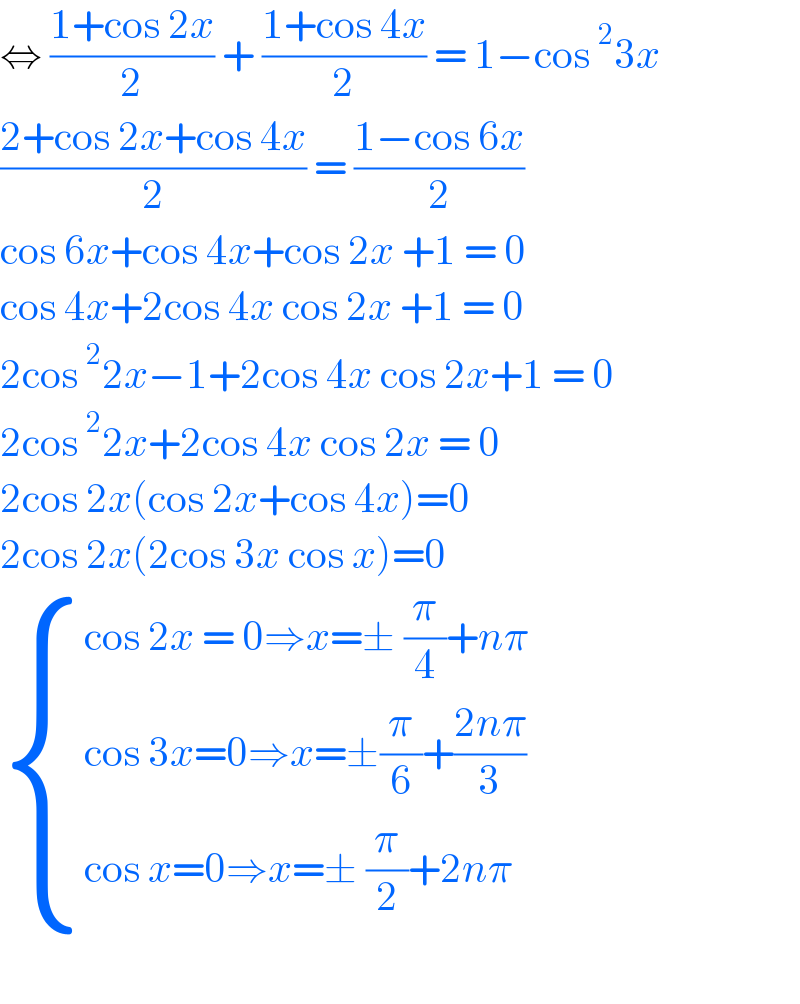
⇔ ((1+cos 2x)/2) + ((1+cos 4x)/2) = 1−cos^2 3x ((2+cos 2x+cos 4x)/2) = ((1−cos 6x)/2) cos 6x+cos 4x+cos 2x +1 = 0 cos 4x+2cos 4x cos 2x +1 = 0 2cos^2 2x−1+2cos 4x cos 2x+1 = 0 2cos^2 2x+2cos 4x cos 2x = 0 2cos 2x(cos 2x+cos 4x)=0 2cos 2x(2cos 3x cos x)=0 { ((cos 2x = 0⇒x=± (π/4)+nπ)),((cos 3x=0⇒x=±(π/6)+((2nπ)/3))),((cos x=0⇒x=± (π/2)+2nπ)) :}
$$\Leftrightarrow\:\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}\:+\:\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{2}}\:=\:\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{x} \\ $$$$\frac{\mathrm{2}+\mathrm{cos}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{2}}\:=\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{6}{x}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\mathrm{6}{x}+\mathrm{cos}\:\mathrm{4}{x}+\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{4}{x}+\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}+\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{2}{x}+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{2}{x}\:=\:\mathrm{0} \\ $$$$\mathrm{2cos}\:\mathrm{2}{x}\left(\mathrm{cos}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{4}{x}\right)=\mathrm{0} \\ $$$$\mathrm{2cos}\:\mathrm{2}{x}\left(\mathrm{2cos}\:\mathrm{3}{x}\:\mathrm{cos}\:{x}\right)=\mathrm{0}\: \\ $$$$\begin{cases}{\mathrm{cos}\:\mathrm{2}{x}\:=\:\mathrm{0}\Rightarrow{x}=\pm\:\frac{\pi}{\mathrm{4}}+{n}\pi}\\{\mathrm{cos}\:\mathrm{3}{x}=\mathrm{0}\Rightarrow{x}=\pm\frac{\pi}{\mathrm{6}}+\frac{\mathrm{2}{n}\pi}{\mathrm{3}}}\\{\mathrm{cos}\:{x}=\mathrm{0}\Rightarrow{x}=\pm\:\frac{\pi}{\mathrm{2}}+\mathrm{2}{n}\pi}\end{cases} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *