The-square-ABCD-has-side-equal-to-1-and-the-distance-AP-is-1-8-Calculate-the-side-of-the-equilateral-triangle-PMN-inscribed-in-the-square-

Question Number 68831 by Maclaurin Stickker last updated on 15/Sep/19

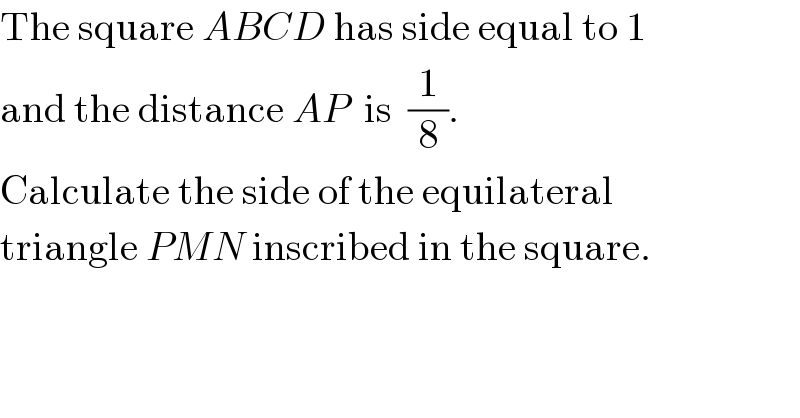
$$\mathrm{The}\:\mathrm{square}\:{ABCD}\:\mathrm{has}\:\mathrm{side}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{distance}\:{AP}\:\:\mathrm{is}\:\:\frac{\mathrm{1}}{\mathrm{8}}. \\ $$$$\mathrm{Calculate}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equilateral} \\ $$$$\mathrm{triangle}\:{PMN}\:\mathrm{inscribed}\:\mathrm{in}\:\mathrm{the}\:\mathrm{square}. \\ $$

Commented by Maclaurin Stickker last updated on 15/Sep/19

Commented by ajfour last updated on 16/Sep/19

let AP =(1/8)=a triangle side s, side of square 1. scos α=1 DP = scos ((π/6)−α)=1−a ⇒ ((√3)/2)+((s/2))sin α=1−a s(√(1−(1/s^2 )))=(7/4)−(√3) s^2 −1=((7/4)−(√3))^2 s^2 =((49)/(16))+3−((7(√3))/2)+1 s=((√(113−56(√3)))/4) .

$${let}\:{AP}\:=\frac{\mathrm{1}}{\mathrm{8}}={a} \\ $$$${triangle}\:{side}\:{s},\:{side}\:{of}\:{square}\:\mathrm{1}. \\ $$$${s}\mathrm{cos}\:\alpha=\mathrm{1} \\ $$$${DP}\:=\:{s}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}−\alpha\right)=\mathrm{1}−{a} \\ $$$$\Rightarrow\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\left(\frac{{s}}{\mathrm{2}}\right)\mathrm{sin}\:\alpha=\mathrm{1}−{a} \\ $$$${s}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{s}^{\mathrm{2}} }}=\frac{\mathrm{7}}{\mathrm{4}}−\sqrt{\mathrm{3}} \\ $$$${s}^{\mathrm{2}} −\mathrm{1}=\left(\frac{\mathrm{7}}{\mathrm{4}}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\:\:{s}^{\mathrm{2}} =\frac{\mathrm{49}}{\mathrm{16}}+\mathrm{3}−\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{1} \\ $$$$\:{s}=\frac{\sqrt{\mathrm{113}−\mathrm{56}\sqrt{\mathrm{3}}}}{\mathrm{4}}\:. \\ $$

Commented by Maclaurin Stickker last updated on 16/Sep/19

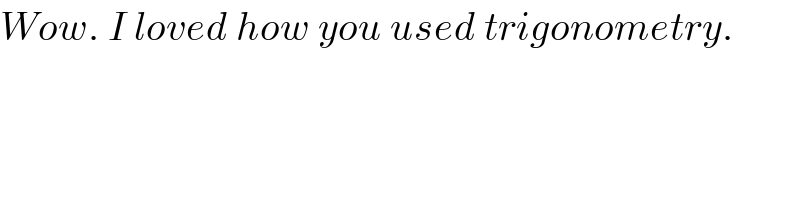
$${Wow}.\:{I}\:{loved}\:{how}\:{you}\:{used}\:{trigonometry}. \\ $$

Answered by MJS last updated on 16/Sep/19

P= ((0),((1/8)) ) M= ((1),(y) ) N= ((x),(1) ) ∣PM∣^2 =∣PN∣^2 =∣MN∣^2 y^2 −(1/4)y+((65)/(64))=x^2 +((49)/(64))=x^2 +y^2 −2x−2y+2 y^2 −(1/4)y+((65)/(64))=x^2 +y^2 −2x−2y+2 ⇒ y=(4/7)x^2 −(8/7)x+(9/(16)) y^2 −(1/4)y+((65)/(64))=x^2 +((49)/(64)) ⇒ x^4 −4x^3 +((79)/(32))x^2 −((49)/(16))x+((5341)/(4096))=0 (x^2 +((49)/(64)))(x^2 −4x+((109)/(64)))=0 x∈[0; 1] ⇒ x=2−((7(√3))/8) ⇒ y=((15)/8)−(√3) ⇒ side s=((√(113−56(√3)))/4)

$${P}=\begin{pmatrix}{\mathrm{0}}\\{\frac{\mathrm{1}}{\mathrm{8}}}\end{pmatrix}\:\:{M}=\begin{pmatrix}{\mathrm{1}}\\{{y}}\end{pmatrix}\:\:{N}=\begin{pmatrix}{{x}}\\{\mathrm{1}}\end{pmatrix} \\ $$$$\mid{PM}\mid^{\mathrm{2}} =\mid{PN}\mid^{\mathrm{2}} =\mid{MN}\mid^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}{y}+\frac{\mathrm{65}}{\mathrm{64}}={x}^{\mathrm{2}} +\frac{\mathrm{49}}{\mathrm{64}}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}{y}+\mathrm{2} \\ $$$$ \\ $$$${y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}{y}+\frac{\mathrm{65}}{\mathrm{64}}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}{y}+\mathrm{2} \\ $$$$\Rightarrow\:{y}=\frac{\mathrm{4}}{\mathrm{7}}{x}^{\mathrm{2}} −\frac{\mathrm{8}}{\mathrm{7}}{x}+\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$ \\ $$$${y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}{y}+\frac{\mathrm{65}}{\mathrm{64}}={x}^{\mathrm{2}} +\frac{\mathrm{49}}{\mathrm{64}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\frac{\mathrm{79}}{\mathrm{32}}{x}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{16}}{x}+\frac{\mathrm{5341}}{\mathrm{4096}}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{49}}{\mathrm{64}}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\frac{\mathrm{109}}{\mathrm{64}}\right)=\mathrm{0} \\ $$$${x}\in\left[\mathrm{0};\:\mathrm{1}\right]\:\Rightarrow\:{x}=\mathrm{2}−\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{8}}\:\Rightarrow\:{y}=\frac{\mathrm{15}}{\mathrm{8}}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{side}\:{s}=\frac{\sqrt{\mathrm{113}−\mathrm{56}\sqrt{\mathrm{3}}}}{\mathrm{4}} \\ $$

Commented by Maclaurin Stickker last updated on 16/Sep/19

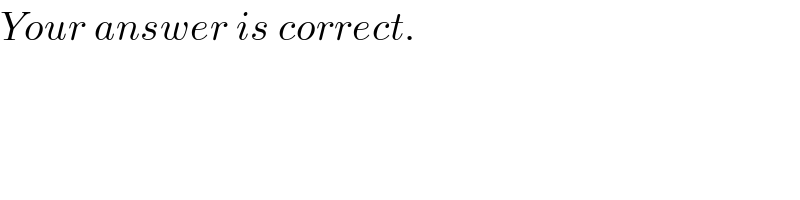
$${Your}\:{answer}\:{is}\:{correct}. \\ $$

Commented by Maclaurin Stickker last updated on 16/Sep/19

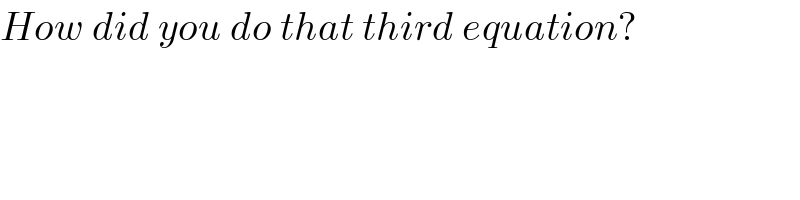
$${How}\:{did}\:{you}\:{do}\:{that}\:{third}\:{equation}? \\ $$

Commented by Maclaurin Stickker last updated on 16/Sep/19

$${Thank}\:{you}!\: \\ $$

Commented by MJS last updated on 16/Sep/19

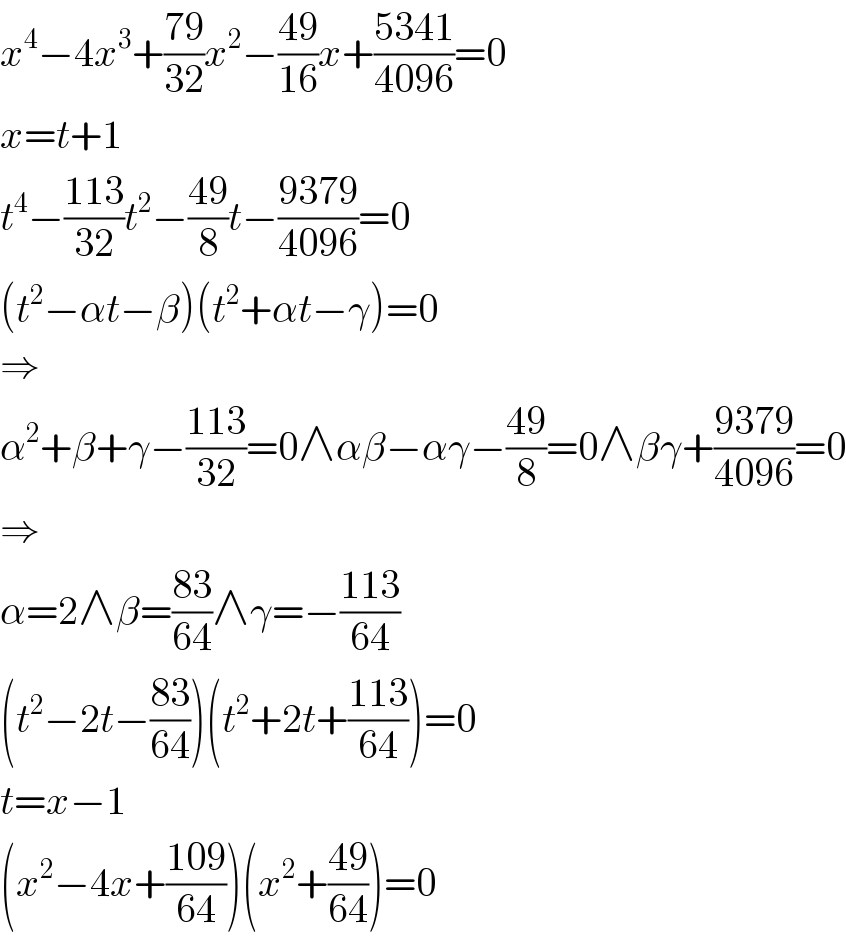
x^4 −4x^3 +((79)/(32))x^2 −((49)/(16))x+((5341)/(4096))=0 x=t+1 t^4 −((113)/(32))t^2 −((49)/8)t−((9379)/(4096))=0 (t^2 −αt−β)(t^2 +αt−γ)=0 ⇒ α^2 +β+γ−((113)/(32))=0∧αβ−αγ−((49)/8)=0∧βγ+((9379)/(4096))=0 ⇒ α=2∧β=((83)/(64))∧γ=−((113)/(64)) (t^2 −2t−((83)/(64)))(t^2 +2t+((113)/(64)))=0 t=x−1 (x^2 −4x+((109)/(64)))(x^2 +((49)/(64)))=0

$${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\frac{\mathrm{79}}{\mathrm{32}}{x}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{16}}{x}+\frac{\mathrm{5341}}{\mathrm{4096}}=\mathrm{0} \\ $$$${x}={t}+\mathrm{1} \\ $$$${t}^{\mathrm{4}} −\frac{\mathrm{113}}{\mathrm{32}}{t}^{\mathrm{2}} −\frac{\mathrm{49}}{\mathrm{8}}{t}−\frac{\mathrm{9379}}{\mathrm{4096}}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\alpha{t}−\beta\right)\left({t}^{\mathrm{2}} +\alpha{t}−\gamma\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\alpha^{\mathrm{2}} +\beta+\gamma−\frac{\mathrm{113}}{\mathrm{32}}=\mathrm{0}\wedge\alpha\beta−\alpha\gamma−\frac{\mathrm{49}}{\mathrm{8}}=\mathrm{0}\wedge\beta\gamma+\frac{\mathrm{9379}}{\mathrm{4096}}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\alpha=\mathrm{2}\wedge\beta=\frac{\mathrm{83}}{\mathrm{64}}\wedge\gamma=−\frac{\mathrm{113}}{\mathrm{64}} \\ $$$$\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\frac{\mathrm{83}}{\mathrm{64}}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}+\frac{\mathrm{113}}{\mathrm{64}}\right)=\mathrm{0} \\ $$$${t}={x}−\mathrm{1} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\frac{\mathrm{109}}{\mathrm{64}}\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{49}}{\mathrm{64}}\right)=\mathrm{0} \\ $$

Facebook Tweet Pin

The-square-ABCD-has-side-equal-to-1-and-the-distance-AP-is-1-8-Calculate-the-side-of-the-equilateral-triangle-PMN-inscribed-in-the-square-

Leave a Reply Cancel reply