Menu Close

The-straight-line-x-y-1-0-meets-the-cicle-x-2-y-2-6x-8y-0-at-A-and-B-Then-find-the-equation-of-circle-of-which-AB-is-diameter-

Tinku Tara 0 Comments
Pin




Question Number 134287 by EDWIN88 last updated on 02/Mar/21
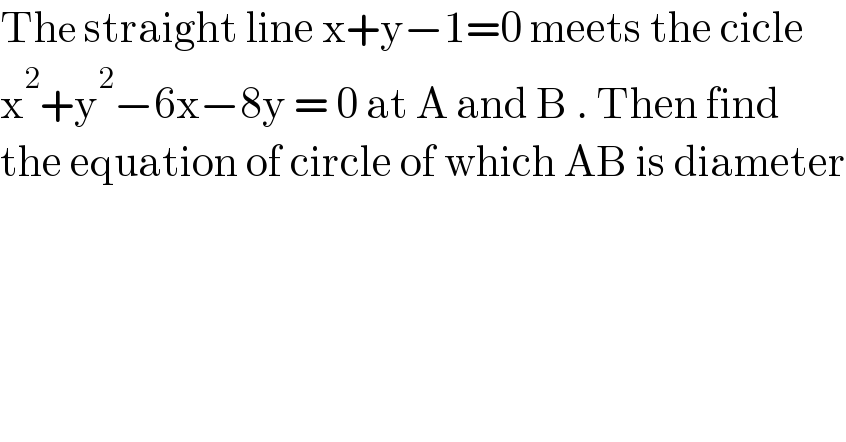
The straight line x+y−1=0 meets the cicle x^2 +y^2 −6x−8y = 0 at A and B . Then find the equation of circle of which AB is diameter
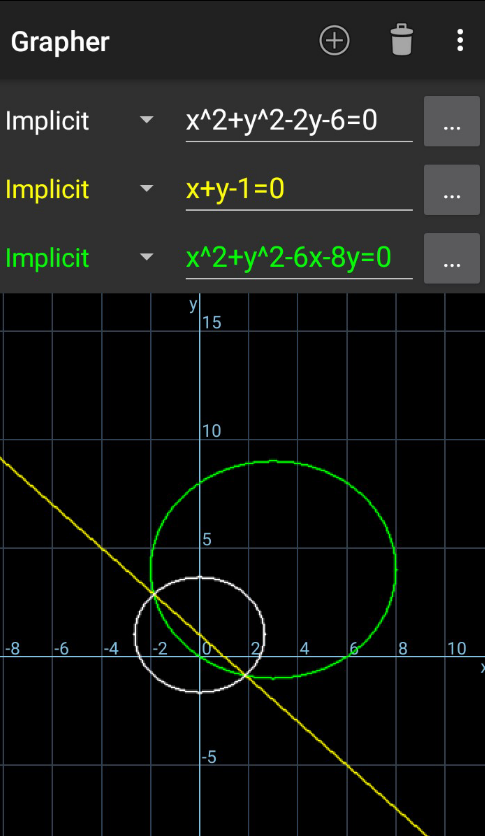
$$\mathrm{The}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{x}+\mathrm{y}−\mathrm{1}=\mathrm{0}\:\mathrm{meets}\:\mathrm{the}\:\mathrm{cicle} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{6x}−\mathrm{8y}\:=\:\mathrm{0}\:\mathrm{at}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:.\:\mathrm{Then}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{which}\:\mathrm{AB}\:\mathrm{is}\:\mathrm{diameter} \\ $$
Answered by bramlexs22 last updated on 02/Mar/21
let the requires equation of circle is C_1 +λℓ = 0 ; then ⇒x^2 +y^2 −6x−8y+λ(x+y−1)=0 ⇒x^2 +y^2 +(λ−6)x+(λ−8)y−λ=0 with center point at (((6−λ)/2) ,((8−λ)/2)) since the center point lie on line x+y−1=0 ⇒we find ((6−λ)/2)+((8−λ)/2) =1 ⇒14−2λ = 2 ; λ=6. therefore the equation of circle of which AB is diameter ≡ x^2 +y^2 −2y−6 = 0
$$\mathrm{let}\:\mathrm{the}\:\mathrm{requires}\:\mathrm{equation}\:\mathrm{of}\: \\ $$$$\mathrm{circle}\:\mathrm{is}\:\mathrm{C}_{\mathrm{1}} +\lambda\ell\:=\:\mathrm{0}\:;\:\mathrm{then} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{8}{y}+\lambda\left({x}+{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\left(\lambda−\mathrm{6}\right)\mathrm{x}+\left(\lambda−\mathrm{8}\right)\mathrm{y}−\lambda=\mathrm{0} \\ $$$$\mathrm{with}\:\mathrm{center}\:\mathrm{point}\:\mathrm{at}\:\left(\frac{\mathrm{6}−\lambda}{\mathrm{2}}\:,\frac{\mathrm{8}−\lambda}{\mathrm{2}}\right) \\ $$$$\mathrm{since}\:\mathrm{the}\:\mathrm{center}\:\mathrm{point}\:\mathrm{lie}\:\mathrm{on}\:\mathrm{line} \\ $$$$\mathrm{x}+\mathrm{y}−\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{we}\:\mathrm{find}\:\frac{\mathrm{6}−\lambda}{\mathrm{2}}+\frac{\mathrm{8}−\lambda}{\mathrm{2}}\:=\mathrm{1} \\ $$$$\Rightarrow\mathrm{14}−\mathrm{2}\lambda\:=\:\mathrm{2}\:;\:\lambda=\mathrm{6}. \\ $$$$\mathrm{therefore}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{circle} \\ $$$$\mathrm{of}\:\mathrm{which}\:\mathrm{AB}\:\mathrm{is}\:\mathrm{diameter}\:\equiv \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2y}−\mathrm{6}\:=\:\mathrm{0}\: \\ $$$$ \\ $$
Commented by bramlexs22 last updated on 02/Mar/21
Answered by EDWIN88 last updated on 02/Mar/21
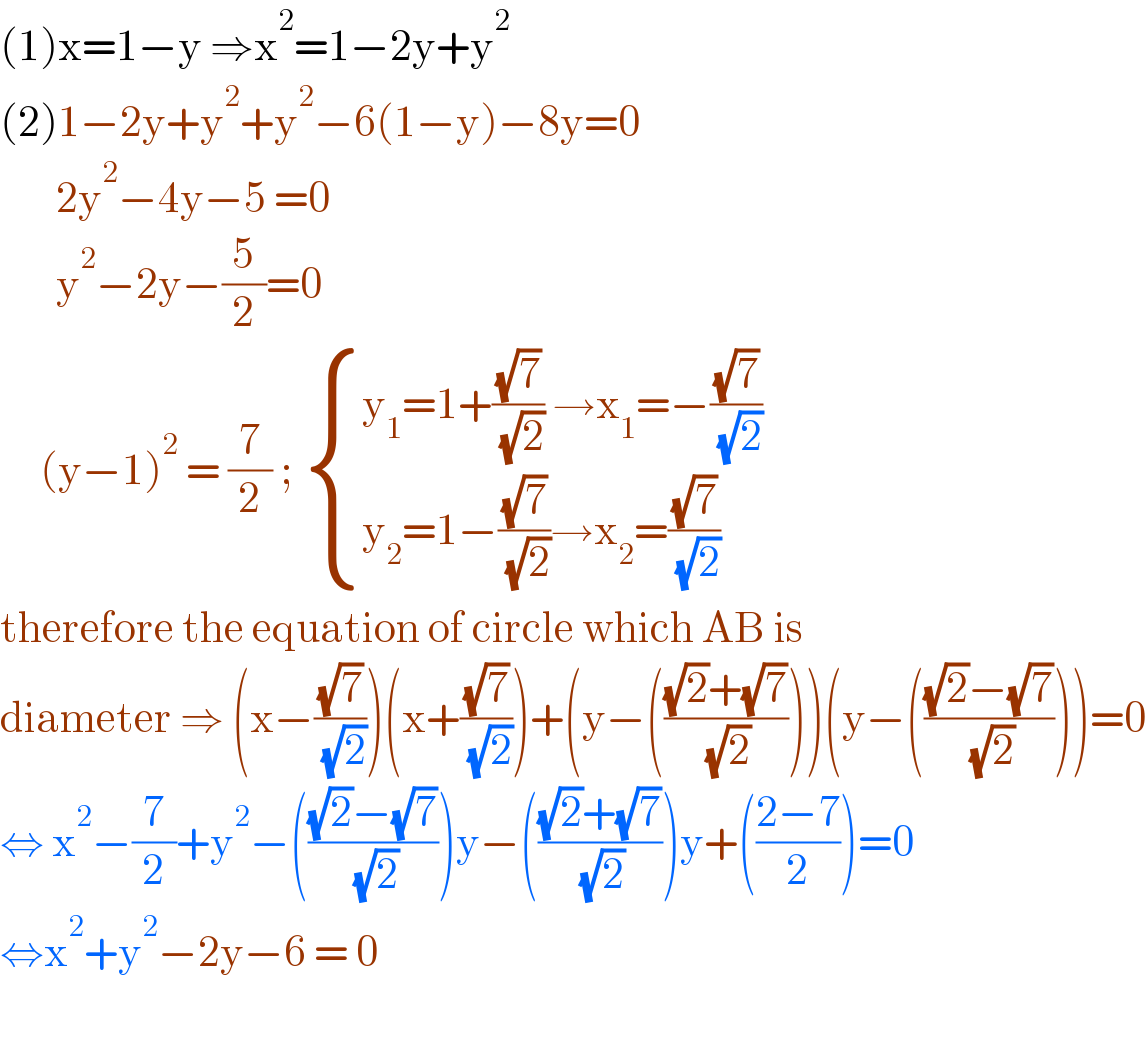
(1)x=1−y ⇒x^2 =1−2y+y^2 (2)1−2y+y^2 +y^2 −6(1−y)−8y=0 2y^2 −4y−5 =0 y^2 −2y−(5/2)=0 (y−1)^2 = (7/2) ; { ((y_1 =1+((√7)/( (√2))) →x_1 =−((√7)/( (√2))))),((y_2 =1−((√7)/( (√2)))→x_2 =((√7)/( (√2))))) :} therefore the equation of circle which AB is diameter ⇒ (x−((√7)/( (√2))))(x+((√7)/( (√2))))+(y−((((√2)+(√7))/( (√2)))))(y−((((√2)−(√7))/( (√2)))))=0 ⇔ x^2 −(7/2)+y^2 −((((√2)−(√7))/( (√2))))y−((((√2)+(√7))/( (√2))))y+(((2−7)/2))=0 ⇔x^2 +y^2 −2y−6 = 0
$$\left(\mathrm{1}\right)\mathrm{x}=\mathrm{1}−\mathrm{y}\:\Rightarrow\mathrm{x}^{\mathrm{2}} =\mathrm{1}−\mathrm{2y}+\mathrm{y}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\mathrm{1}−\mathrm{2y}+\mathrm{y}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{6}\left(\mathrm{1}−\mathrm{y}\right)−\mathrm{8y}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{2y}^{\mathrm{2}} −\mathrm{4y}−\mathrm{5}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{y}^{\mathrm{2}} −\mathrm{2y}−\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{0} \\ $$$$\:\:\:\:\:\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{7}}{\mathrm{2}}\:;\:\begin{cases}{\mathrm{y}_{\mathrm{1}} =\mathrm{1}+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\:\rightarrow\mathrm{x}_{\mathrm{1}} =−\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}}\\{\mathrm{y}_{\mathrm{2}} =\mathrm{1}−\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\rightarrow\mathrm{x}_{\mathrm{2}} =\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}}\end{cases} \\ $$$$\mathrm{therefore}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{which}\:\mathrm{AB}\:\mathrm{is}\: \\ $$$$\mathrm{diameter}\:\Rightarrow\:\left(\mathrm{x}−\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\right)\left(\mathrm{x}+\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\right)+\left(\mathrm{y}−\left(\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\right)\right)\left(\mathrm{y}−\left(\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\right)\right)=\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{7}}{\mathrm{2}}+\mathrm{y}^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\right)\mathrm{y}−\left(\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}}\right)\mathrm{y}+\left(\frac{\mathrm{2}−\mathrm{7}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2y}−\mathrm{6}\:=\:\mathrm{0}\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *