Menu Close

The-sums-of-the-first-n-terms-of-two-AP-s-are-in-the-ratio-3n-31-5n-3-Show-that-their-9-th-terms-are-equal-

Tinku Tara 0 Comments
Pin




Question Number 2619 by Rasheed Soomro last updated on 23/Nov/15
The sums of the first n terms of two AP ′s are in the ratio 3n+31 : 5n−3 . Show that their 9^(th) terms are equal.
$${The}\:{sums}\:{of}\:{the}\:{first}\:\:{n}\:\:\:{terms}\:{of}\:{two}\:{AP}\:'{s}\:{are} \\ $$$${in}\:{the}\:{ratio}\:\:\mathrm{3}{n}+\mathrm{31}\::\:\:\mathrm{5}{n}−\mathrm{3}\:.\:{Show}\:{that}\:{their}\:\mathrm{9}^{{th}} \:{terms} \\ $$$${are}\:{equal}. \\ $$
Commented by Yozzi last updated on 24/Nov/15
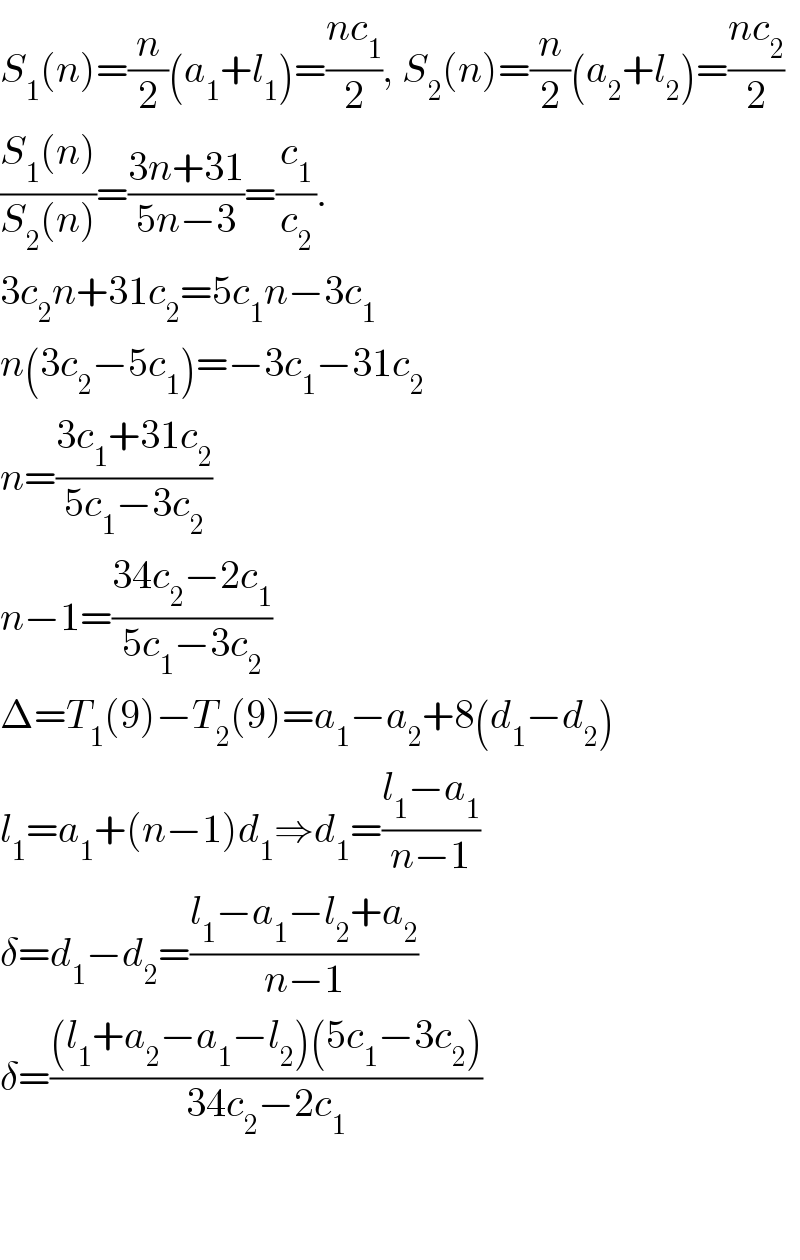
S_1 (n)=(n/2)(a_1 +l_1 )=((nc_1 )/2), S_2 (n)=(n/2)(a_2 +l_2 )=((nc_2 )/2) ((S_1 (n))/(S_2 (n)))=((3n+31)/(5n−3))=(c_1 /c_2 ). 3c_2 n+31c_2 =5c_1 n−3c_1 n(3c_2 −5c_1 )=−3c_1 −31c_2 n=((3c_1 +31c_2 )/(5c_1 −3c_2 )) n−1=((34c_2 −2c_1 )/(5c_1 −3c_2 )) Δ=T_1 (9)−T_2 (9)=a_1 −a_2 +8(d_1 −d_2 ) l_1 =a_1 +(n−1)d_1 ⇒d_1 =((l_1 −a_1 )/(n−1)) δ=d_1 −d_2 =((l_1 −a_1 −l_2 +a_2 )/(n−1)) δ=(((l_1 +a_2 −a_1 −l_2 )(5c_1 −3c_2 ))/(34c_2 −2c_1 ))
$${S}_{\mathrm{1}} \left({n}\right)=\frac{{n}}{\mathrm{2}}\left({a}_{\mathrm{1}} +{l}_{\mathrm{1}} \right)=\frac{{nc}_{\mathrm{1}} }{\mathrm{2}},\:{S}_{\mathrm{2}} \left({n}\right)=\frac{{n}}{\mathrm{2}}\left({a}_{\mathrm{2}} +{l}_{\mathrm{2}} \right)=\frac{{nc}_{\mathrm{2}} }{\mathrm{2}} \\ $$$$\frac{{S}_{\mathrm{1}} \left({n}\right)}{{S}_{\mathrm{2}} \left({n}\right)}=\frac{\mathrm{3}{n}+\mathrm{31}}{\mathrm{5}{n}−\mathrm{3}}=\frac{{c}_{\mathrm{1}} }{{c}_{\mathrm{2}} }. \\ $$$$\mathrm{3}{c}_{\mathrm{2}} {n}+\mathrm{31}{c}_{\mathrm{2}} =\mathrm{5}{c}_{\mathrm{1}} {n}−\mathrm{3}{c}_{\mathrm{1}} \\ $$$${n}\left(\mathrm{3}{c}_{\mathrm{2}} −\mathrm{5}{c}_{\mathrm{1}} \right)=−\mathrm{3}{c}_{\mathrm{1}} −\mathrm{31}{c}_{\mathrm{2}} \\ $$$${n}=\frac{\mathrm{3}{c}_{\mathrm{1}} +\mathrm{31}{c}_{\mathrm{2}} }{\mathrm{5}{c}_{\mathrm{1}} −\mathrm{3}{c}_{\mathrm{2}} } \\ $$$${n}−\mathrm{1}=\frac{\mathrm{34}{c}_{\mathrm{2}} −\mathrm{2}{c}_{\mathrm{1}} }{\mathrm{5}{c}_{\mathrm{1}} −\mathrm{3}{c}_{\mathrm{2}} } \\ $$$$\Delta={T}_{\mathrm{1}} \left(\mathrm{9}\right)−{T}_{\mathrm{2}} \left(\mathrm{9}\right)={a}_{\mathrm{1}} −{a}_{\mathrm{2}} +\mathrm{8}\left({d}_{\mathrm{1}} −{d}_{\mathrm{2}} \right) \\ $$$${l}_{\mathrm{1}} ={a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} \Rightarrow{d}_{\mathrm{1}} =\frac{{l}_{\mathrm{1}} −{a}_{\mathrm{1}} }{{n}−\mathrm{1}} \\ $$$$\delta={d}_{\mathrm{1}} −{d}_{\mathrm{2}} =\frac{{l}_{\mathrm{1}} −{a}_{\mathrm{1}} −{l}_{\mathrm{2}} +{a}_{\mathrm{2}} }{{n}−\mathrm{1}} \\ $$$$\delta=\frac{\left({l}_{\mathrm{1}} +{a}_{\mathrm{2}} −{a}_{\mathrm{1}} −{l}_{\mathrm{2}} \right)\left(\mathrm{5}{c}_{\mathrm{1}} −\mathrm{3}{c}_{\mathrm{2}} \right)}{\mathrm{34}{c}_{\mathrm{2}} −\mathrm{2}{c}_{\mathrm{1}} } \\ $$$$ \\ $$$$ \\ $$
Answered by prakash jain last updated on 24/Nov/15
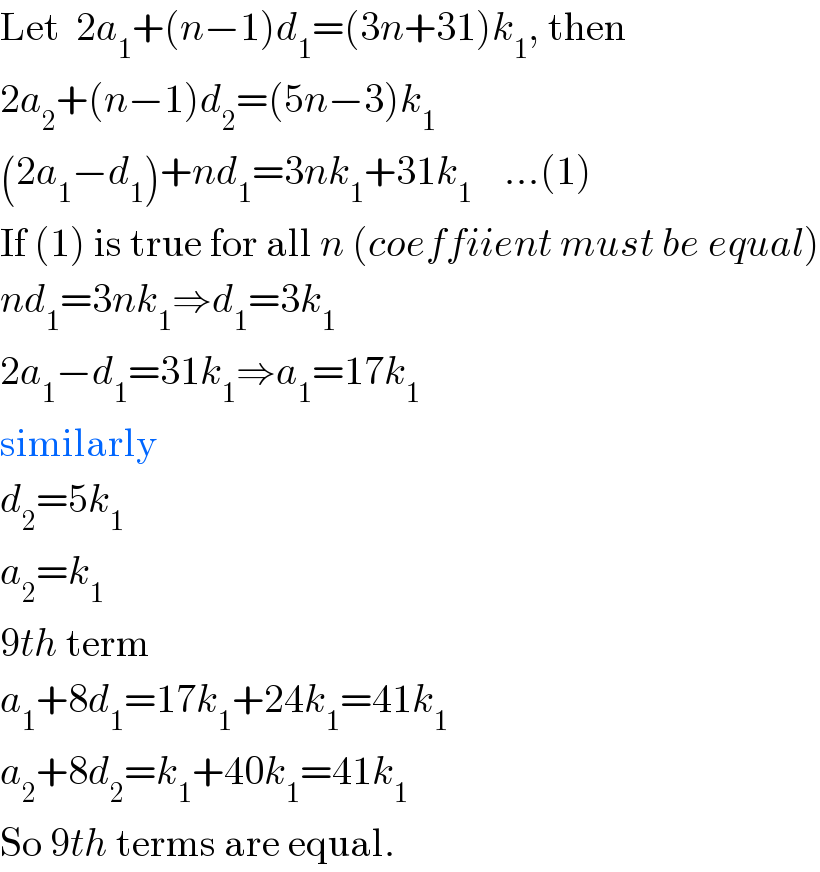
Let 2a_1 +(n−1)d_1 =(3n+31)k_1 , then 2a_2 +(n−1)d_2 =(5n−3)k_1 (2a_1 −d_1 )+nd_1 =3nk_1 +31k_1 ...(1) If (1) is true for all n (coeffiient must be equal) nd_1 =3nk_1 ⇒d_1 =3k_1 2a_1 −d_1 =31k_1 ⇒a_1 =17k_1 similarly d_2 =5k_1 a_2 =k_1 9th term a_1 +8d_1 =17k_1 +24k_1 =41k_1 a_2 +8d_2 =k_1 +40k_1 =41k_1 So 9th terms are equal.
$$\mathrm{Let}\:\:\mathrm{2}{a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} =\left(\mathrm{3}{n}+\mathrm{31}\right){k}_{\mathrm{1}} ,\:\mathrm{then} \\ $$$$\mathrm{2}{a}_{\mathrm{2}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{2}} =\left(\mathrm{5}{n}−\mathrm{3}\right){k}_{\mathrm{1}} \\ $$$$\left(\mathrm{2}{a}_{\mathrm{1}} −{d}_{\mathrm{1}} \right)+{nd}_{\mathrm{1}} =\mathrm{3}{nk}_{\mathrm{1}} +\mathrm{31}{k}_{\mathrm{1}} \:\:\:\:…\left(\mathrm{1}\right) \\ $$$$\mathrm{If}\:\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:{n}\:\left({coeffiient}\:{must}\:{be}\:{equal}\right) \\ $$$${nd}_{\mathrm{1}} =\mathrm{3}{nk}_{\mathrm{1}} \Rightarrow{d}_{\mathrm{1}} =\mathrm{3}{k}_{\mathrm{1}} \\ $$$$\mathrm{2}{a}_{\mathrm{1}} −{d}_{\mathrm{1}} =\mathrm{31}{k}_{\mathrm{1}} \Rightarrow{a}_{\mathrm{1}} =\mathrm{17}{k}_{\mathrm{1}} \\ $$$$\mathrm{similarly} \\ $$$${d}_{\mathrm{2}} =\mathrm{5}{k}_{\mathrm{1}} \\ $$$${a}_{\mathrm{2}} ={k}_{\mathrm{1}} \\ $$$$\mathrm{9}{th}\:\mathrm{term} \\ $$$${a}_{\mathrm{1}} +\mathrm{8}{d}_{\mathrm{1}} =\mathrm{17}{k}_{\mathrm{1}} +\mathrm{24}{k}_{\mathrm{1}} =\mathrm{41}{k}_{\mathrm{1}} \\ $$$${a}_{\mathrm{2}} +\mathrm{8}{d}_{\mathrm{2}} ={k}_{\mathrm{1}} +\mathrm{40}{k}_{\mathrm{1}} =\mathrm{41}{k}_{\mathrm{1}} \\ $$$$\mathrm{So}\:\mathrm{9}{th}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{equal}. \\ $$
Answered by Rasheed Soomro last updated on 24/Nov/15
Without repeating understood things (((n/2)[2a_1 +(n−1)d_1 ])/((n/2)[2a_2 +(n−1)d_2 ]))=((3n+31)/(5n−3)) [Given] a_1 +8d_(1 ) (T_9 )=a_2 +8d_2 (t_9 ) [Required] (((n/2)[2a_1 +(n−1)d_1 ])/((n/2)[2a_2 +(n−1)d_2 ]))=((3n+31)/(5n−3)) Our goal: To achieve a_1 +8d_(1 ) in numerator and a_2 +8d_2 in denominator because we want to determine relation between T_9 and t_9 . ⇒((2a_1 +(n−1)d_1 )/(2a_2 +(n−1)d_2 ))=((3n+31)/(5n−3)) ⇒((2[a_1 +(((n−1)/2))d_1 ])/(2[a_2 +(((n−1)/2))d_2 ]))=((3n+31)/(5n−3)) ⇒((a_1 +(((n−1)/2))d_1 )/(a_2 +(((n−1)/2))d_2 ))=((3n+31)/(5n−3)) We want 8 in place of ((n−1)/2) ∴ ((n−1)/2)=8⇒n=17 ⇒((a_1 +8d_1 )/(a_2 +8d_2 ))=((3(17)+31)/(5(17)−3))=((82)/(82))=1 ∴ T_9 =t_9
$${Without}\:{repeating}\:{understood}\:{things} \\ $$$$\frac{\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} \right]}{\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}_{\mathrm{2}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{2}} \right]}=\frac{\mathrm{3}{n}+\mathrm{31}}{\mathrm{5}{n}−\mathrm{3}}\:\:\:\:\left[{Given}\right] \\ $$$${a}_{\mathrm{1}} +\mathrm{8}{d}_{\mathrm{1}\:} \left({T}_{\mathrm{9}} \right)={a}_{\mathrm{2}} +\mathrm{8}{d}_{\mathrm{2}} \left({t}_{\mathrm{9}} \right)\:\:\:\:\:\:\:\:\:\left[{Required}\right]\:\:\:\: \\ $$$$\frac{\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} \right]}{\frac{{n}}{\mathrm{2}}\left[\mathrm{2}{a}_{\mathrm{2}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{2}} \right]}=\frac{\mathrm{3}{n}+\mathrm{31}}{\mathrm{5}{n}−\mathrm{3}} \\ $$$$\mathcal{O}{ur}\:{goal}:\:{To}\:{achieve}\:{a}_{\mathrm{1}} +\mathrm{8}{d}_{\mathrm{1}\:} {in}\:{numerator} \\ $$$${and}\:{a}_{\mathrm{2}} +\mathrm{8}{d}_{\mathrm{2}} \:{in}\:{denominator}\:{because}\:{we}\:{want} \\ $$$${to}\:{determine}\:{relation}\:{between}\:{T}_{\mathrm{9}} \:{and}\:{t}_{\mathrm{9}} \:. \\ $$$$\Rightarrow\frac{\mathrm{2}{a}_{\mathrm{1}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{1}} }{\mathrm{2}{a}_{\mathrm{2}} +\left({n}−\mathrm{1}\right){d}_{\mathrm{2}} }=\frac{\mathrm{3}{n}+\mathrm{31}}{\mathrm{5}{n}−\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{2}\left[{a}_{\mathrm{1}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{1}} \right]}{\mathrm{2}\left[{a}_{\mathrm{2}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{2}} \right]}=\frac{\mathrm{3}{n}+\mathrm{31}}{\mathrm{5}{n}−\mathrm{3}} \\ $$$$\Rightarrow\frac{{a}_{\mathrm{1}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{1}} }{{a}_{\mathrm{2}} +\left(\frac{{n}−\mathrm{1}}{\mathrm{2}}\right){d}_{\mathrm{2}} }=\frac{\mathrm{3}{n}+\mathrm{31}}{\mathrm{5}{n}−\mathrm{3}} \\ $$$${We}\:{want}\:\mathrm{8}\:{in}\:{place}\:{of}\:\frac{{n}−\mathrm{1}}{\mathrm{2}} \\ $$$$\therefore\:\:\frac{{n}−\mathrm{1}}{\mathrm{2}}=\mathrm{8}\Rightarrow{n}=\mathrm{17} \\ $$$$\Rightarrow\frac{{a}_{\mathrm{1}} +\mathrm{8}{d}_{\mathrm{1}} }{{a}_{\mathrm{2}} +\mathrm{8}{d}_{\mathrm{2}} }=\frac{\mathrm{3}\left(\mathrm{17}\right)+\mathrm{31}}{\mathrm{5}\left(\mathrm{17}\right)−\mathrm{3}}=\frac{\mathrm{82}}{\mathrm{82}}=\mathrm{1} \\ $$$$\therefore\:{T}_{\mathrm{9}} ={t}_{\mathrm{9}} \\ $$$$ \\ $$$$ \\ $$
Commented by prakash jain last updated on 24/Nov/15
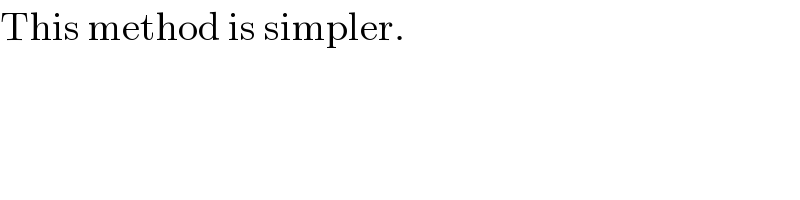
This method is simpler.
$$\mathrm{This}\:\mathrm{method}\:\mathrm{is}\:\mathrm{simpler}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *