Question Number 4633 by sanusihammed last updated on 16/Feb/16

$${The}\:{volume}\:{V}\:\left({in}\:{liters}\right)\:\:{of}\:{petrol}\:{in}\:{a}\:{car}\:{tank}\:{is}\:{decreasing}\: \\ $$$${at}\:{the}\:{rate}\:{of}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{1}}{\mathrm{5}}\:−\:\frac{{m}}{\mathrm{2000}}\right)\:{liters}/{km} \\ $$$$ \\ $$$${After}\:{travelling}\:{m}\:{kilometers}.\:{Assuming}\:{that}\:{V}\:=\:\mathrm{40} \\ $$$${when}\:{m}\:=\:\mathrm{0}.\:{Find}\:{an}\:{expression}\:{for}\:{V}\:\:{in}\:{terms}\:{of}\:{m}. \\ $$$$ \\ $$
Answered by Yozzii last updated on 21/Feb/16
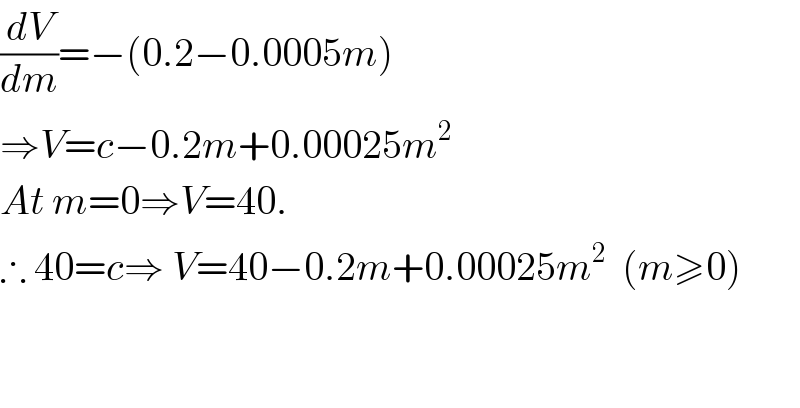
$$\frac{{dV}}{{dm}}=−\left(\mathrm{0}.\mathrm{2}−\mathrm{0}.\mathrm{0005}{m}\right) \\ $$$$\Rightarrow{V}={c}−\mathrm{0}.\mathrm{2}{m}+\mathrm{0}.\mathrm{00025}{m}^{\mathrm{2}} \\ $$$${At}\:{m}=\mathrm{0}\Rightarrow{V}=\mathrm{40}. \\ $$$$\therefore\:\mathrm{40}={c}\Rightarrow\:{V}=\mathrm{40}−\mathrm{0}.\mathrm{2}{m}+\mathrm{0}.\mathrm{00025}{m}^{\mathrm{2}} \:\:\left({m}\geqslant\mathrm{0}\right) \\ $$$$ \\ $$$$ \\ $$
