Question Number 139940 by mathdanisur last updated on 02/May/21

$${There}\:{are}\:\mathrm{4}\:{children}\:{in}\:{the}\:{team}. \\ $$$${Find}\:{the}\:{probability}\:{that}\:{three}\:{are} \\ $$$${girls}\:{and}\:{one}\:{is}\:{a}\:{boy}. \\ $$
Answered by mr W last updated on 02/May/21
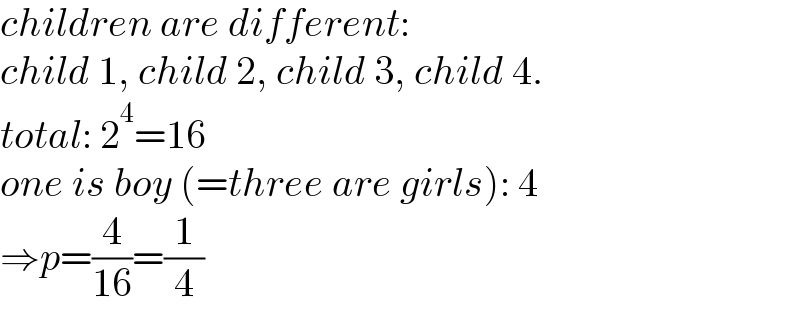
$${children}\:{are}\:{different}: \\ $$$${child}\:\mathrm{1},\:{child}\:\mathrm{2},\:{child}\:\mathrm{3},\:{child}\:\mathrm{4}. \\ $$$${total}:\:\mathrm{2}^{\mathrm{4}} =\mathrm{16} \\ $$$${one}\:{is}\:{boy}\:\left(={three}\:{are}\:{girls}\right):\:\mathrm{4} \\ $$$$\Rightarrow{p}=\frac{\mathrm{4}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mr W last updated on 02/May/21
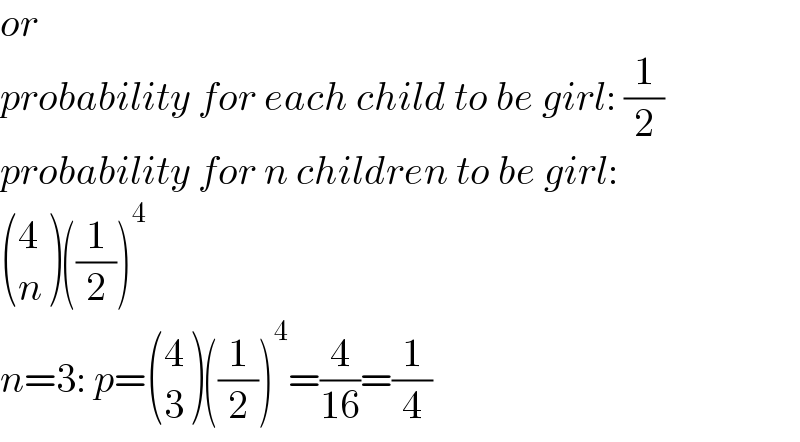
$${or} \\ $$$${probability}\:{for}\:{each}\:{child}\:{to}\:{be}\:{girl}:\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${probability}\:{for}\:{n}\:{children}\:{to}\:{be}\:{girl}:\: \\ $$$$\begin{pmatrix}{\mathrm{4}}\\{{n}}\end{pmatrix}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} \\ $$$${n}=\mathrm{3}:\:{p}=\begin{pmatrix}{\mathrm{4}}\\{\mathrm{3}}\end{pmatrix}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{4}} =\frac{\mathrm{4}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mathdanisur last updated on 02/May/21

$${thanks}\:{Sir} \\ $$
