Question Number 75180 by Rio Michael last updated on 08/Dec/19
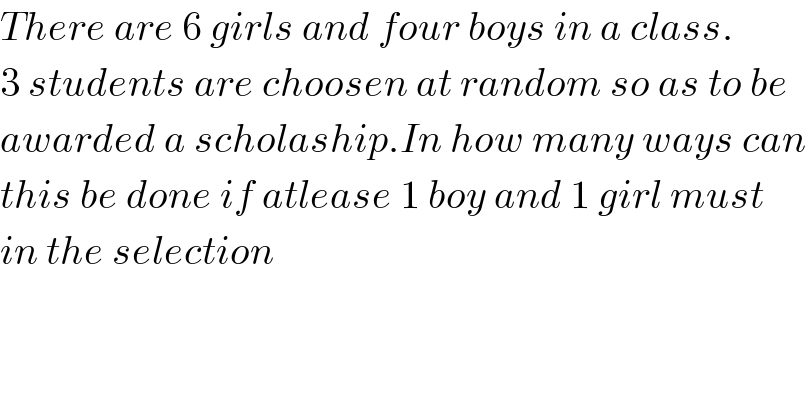
$${There}\:{are}\:\mathrm{6}\:{girls}\:{and}\:{four}\:{boys}\:{in}\:{a}\:{class}. \\ $$$$\mathrm{3}\:{students}\:{are}\:{choosen}\:{at}\:{random}\:{so}\:{as}\:{to}\:{be} \\ $$$${awarded}\:{a}\:{scholaship}.{In}\:{how}\:{many}\:{ways}\:{can} \\ $$$${this}\:{be}\:{done}\:{if}\:{atlease}\:\mathrm{1}\:{boy}\:{and}\:\mathrm{1}\:{girl}\:{must} \\ $$$${in}\:{the}\:{selection} \\ $$$$ \\ $$
Commented by mr W last updated on 08/Dec/19
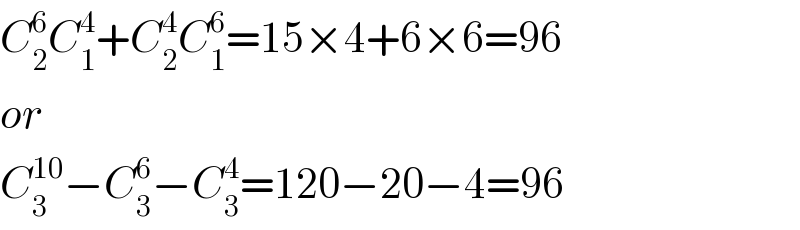
$${C}_{\mathrm{2}} ^{\mathrm{6}} {C}_{\mathrm{1}} ^{\mathrm{4}} +{C}_{\mathrm{2}} ^{\mathrm{4}} {C}_{\mathrm{1}} ^{\mathrm{6}} =\mathrm{15}×\mathrm{4}+\mathrm{6}×\mathrm{6}=\mathrm{96} \\ $$$${or} \\ $$$${C}_{\mathrm{3}} ^{\mathrm{10}} −{C}_{\mathrm{3}} ^{\mathrm{6}} −{C}_{\mathrm{3}} ^{\mathrm{4}} =\mathrm{120}−\mathrm{20}−\mathrm{4}=\mathrm{96} \\ $$
Commented by Rio Michael last updated on 08/Dec/19

$${thanks}\:{sir} \\ $$$${i}\:{prefer}\:{method}\:\mathrm{1} \\ $$
