Question Number 135594 by liberty last updated on 14/Mar/21
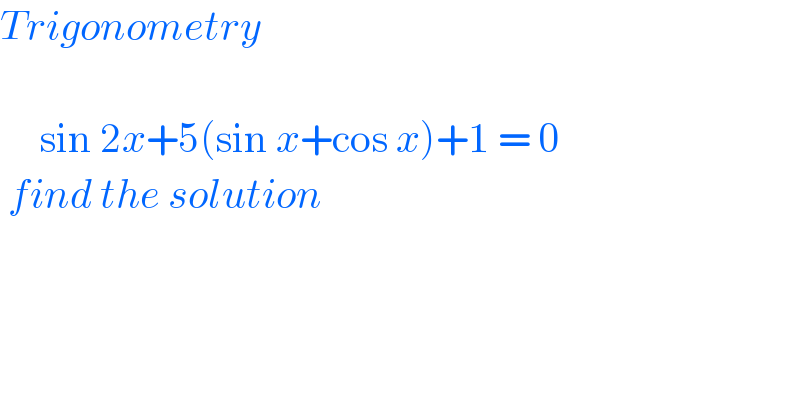
$${Trigonometry} \\ $$$$ \\ $$$$\:\:\:\:\:\mathrm{sin}\:\mathrm{2}{x}+\mathrm{5}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:{find}\:{the}\:{solution} \\ $$
Answered by EDWIN88 last updated on 14/Mar/21
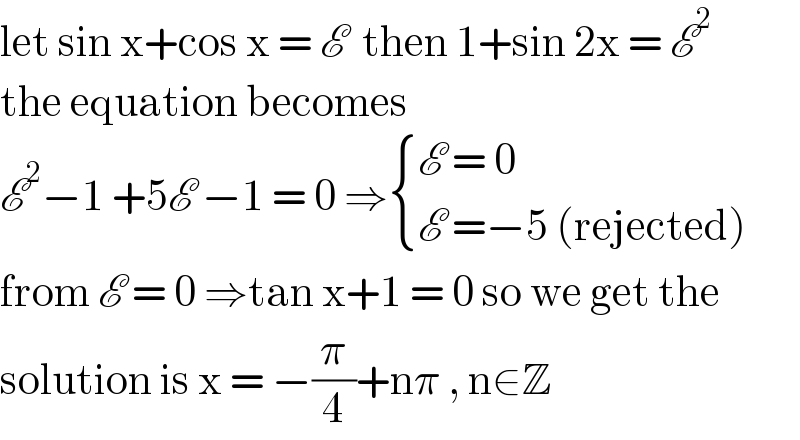
$$\mathrm{let}\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:=\:\mathscr{E}\:\:\mathrm{then}\:\mathrm{1}+\mathrm{sin}\:\mathrm{2x}\:=\:\mathscr{E}^{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{becomes}\: \\ $$$$\mathscr{E}^{\mathrm{2}} −\mathrm{1}\:+\mathrm{5}\mathscr{E}\:−\mathrm{1}\:=\:\mathrm{0}\:\Rightarrow\begin{cases}{\mathscr{E}\:=\:\mathrm{0}}\\{\mathscr{E}\:=−\mathrm{5}\:\left(\mathrm{rejected}\right)}\end{cases} \\ $$$$\mathrm{from}\:\mathscr{E}\:=\:\mathrm{0}\:\Rightarrow\mathrm{tan}\:\mathrm{x}+\mathrm{1}\:=\:\mathrm{0}\:\mathrm{so}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{solution}\:\mathrm{is}\:\mathrm{x}\:=\:−\frac{\pi}{\mathrm{4}}+\mathrm{n}\pi\:,\:\mathrm{n}\in\mathbb{Z} \\ $$
