Question Number 4036 by Rasheed Soomro last updated on 27/Dec/15

Commented by Yozzii last updated on 27/Dec/15
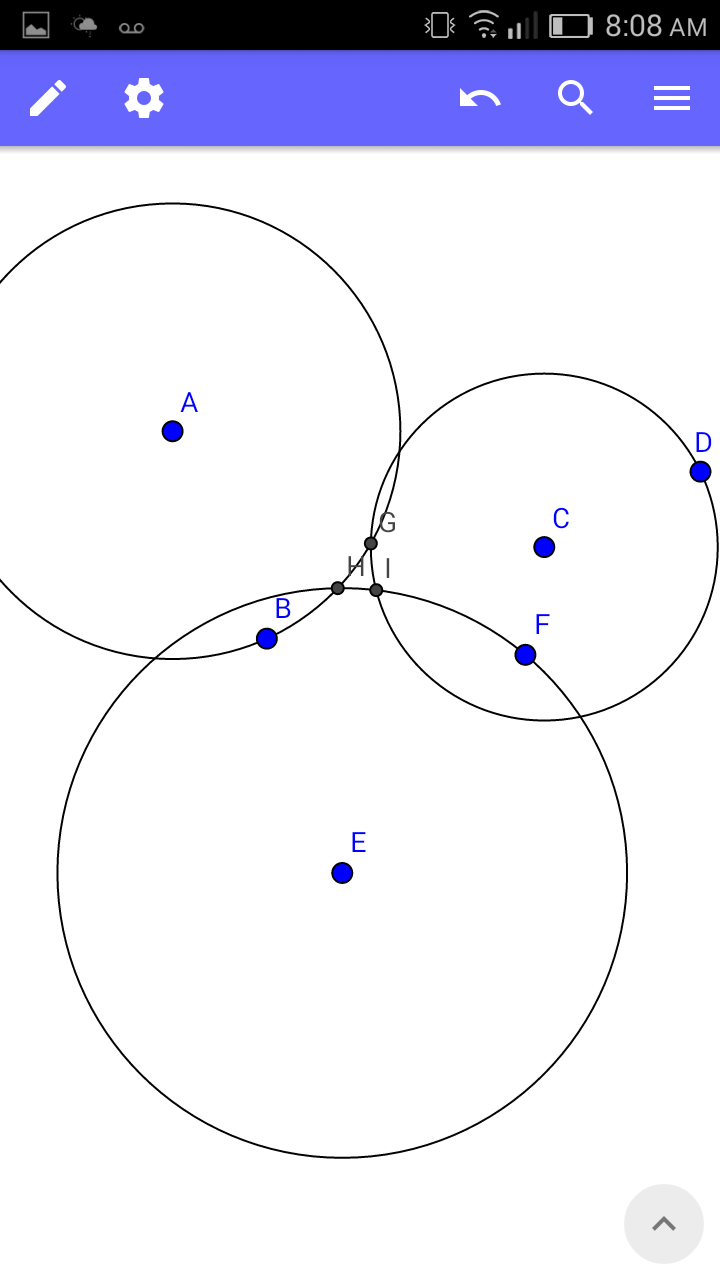
Commented by Yozzii last updated on 27/Dec/15
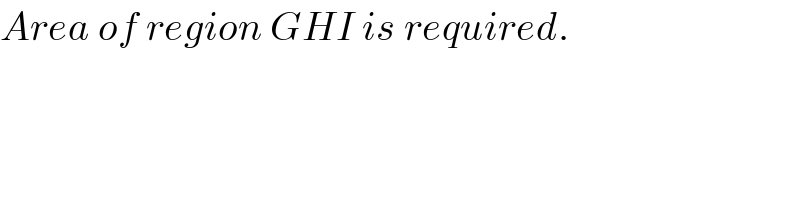
Commented by Rasheed Soomro last updated on 27/Dec/15

Commented by Yozzii last updated on 27/Dec/15
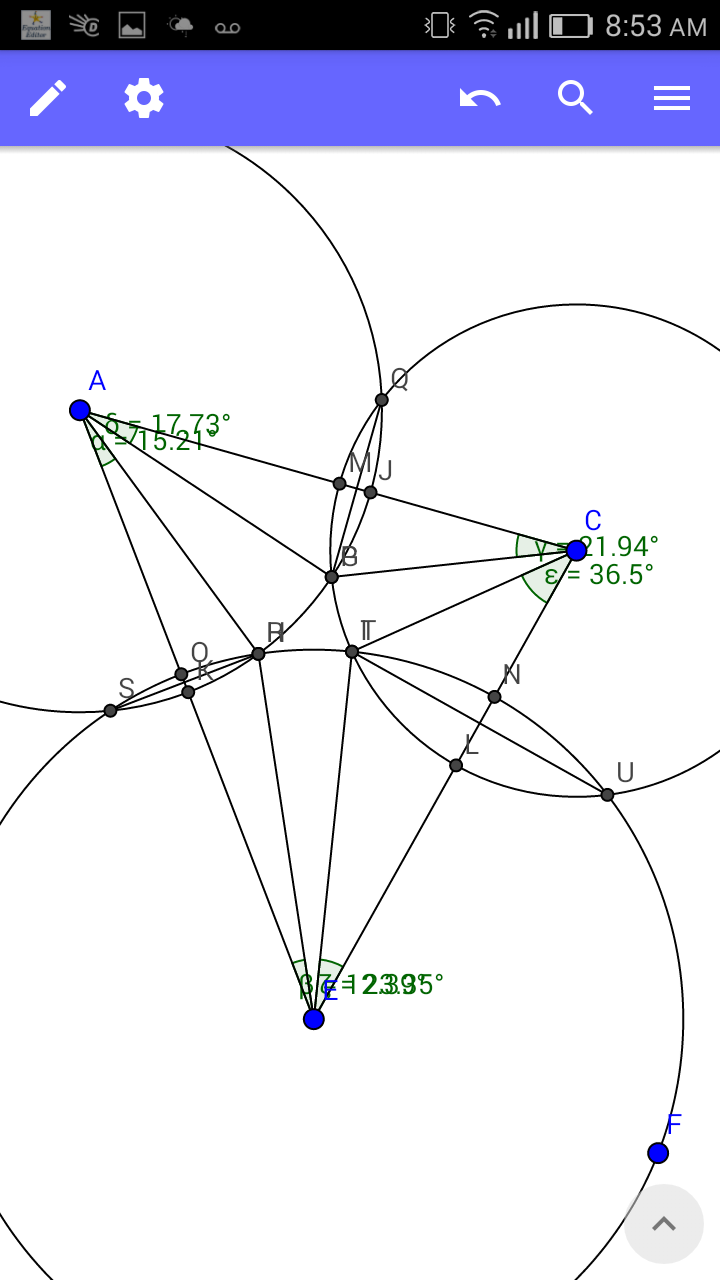
Commented by Yozzii last updated on 27/Dec/15

Commented by Yozzii last updated on 27/Dec/15

Commented by Rasheed Soomro last updated on 27/Dec/15