Menu Close

two-sequences-u-n-and-v-n-for-n-N-is-defined-as-u-0-3-u-n-1-1-2-u-n-v-n-and-v-0-4-v-n-1-1-2-u-n-1-v-n-a-calculate-u-1-v-1-u-2-and

Tinku Tara 0 Comments
Pin




Question Number 76630 by Rio Michael last updated on 28/Dec/19
two sequences , (u_n ) and (v_n ), for n∈N is defined as: { ((u_0 =3)),((u_(n+1) = (1/2)(u_n + v_n ) )) :}and { ((v_0 = 4)),((v_(n+1) = (1/2)(u_(n+1) + v_n ))) :} a) calculate u_1 ,v_1 ,u_2 and v_2 b) Another sequence (w_n ), is defined by w_n = v_n − u_n , ∀ n∈N show that w_n is a convegent geometric sequence. c) Express w_n as a function of n and obtain its limits. d) Study the sense of variation(monotony) of (u_n ) and (v_n ) what can you deduce? e) Consider another sequence t_n defined by t_n = ((u_n + 2v_n )/3) , ∀ n ∈ N show that t_n is a constant sequence f) hence obtain the limit of the sequences (u_n ) and (v_n )
$$\mathrm{two}\:\mathrm{sequences}\:,\:\left({u}_{{n}} \right)\:{and}\:\left({v}_{{n}} \right),\:\mathrm{for}\:{n}\in\mathbb{N}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{as}: \\ $$$$\begin{cases}{{u}_{\mathrm{0}} \:=\mathrm{3}}\\{{u}_{{n}+\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left({u}_{{n}} \:+\:{v}_{{n}} \right)\:\:}\end{cases}\mathrm{and}\:\begin{cases}{{v}_{\mathrm{0}} =\:\mathrm{4}}\\{{v}_{{n}+\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left({u}_{{n}+\mathrm{1}} \:+\:{v}_{{n}} \right)}\end{cases} \\ $$$$\left.{a}\right)\:\mathrm{calculate}\:{u}_{\mathrm{1}} ,{v}_{\mathrm{1}} ,{u}_{\mathrm{2}} \:\mathrm{and}\:{v}_{\mathrm{2}} \\ $$$$\left.{b}\right)\:\mathrm{Another}\:\mathrm{sequence}\:\left({w}_{{n}} \right),\:\mathrm{is}\:\mathrm{defined}\:\mathrm{by}\: \\ $$$$\:{w}_{{n}} \:=\:{v}_{{n}} \:−\:{u}_{{n}} \:,\:\forall\:{n}\in\mathbb{N} \\ $$$$\mathrm{show}\:\mathrm{that}\:{w}_{{n}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{convegent}\:\mathrm{geometric}\:\mathrm{sequence}. \\ $$$$\left.\mathrm{c}\right)\:\mathrm{Express}\:{w}_{{n}} \:\mathrm{as}\:\mathrm{a}\:\mathrm{function}\:\mathrm{of}\:{n}\:\mathrm{and}\:\mathrm{obtain}\:\mathrm{its}\:\mathrm{limits}. \\ $$$$\left.\mathrm{d}\right)\:\mathrm{Study}\:\mathrm{the}\:\mathrm{sense}\:\mathrm{of}\:\mathrm{variation}\left(\mathrm{monotony}\right)\:\:\mathrm{of}\:\left({u}_{{n}} \right)\:\mathrm{and}\:\left({v}_{{n}} \right) \\ $$$$\mathrm{what}\:\mathrm{can}\:\mathrm{you}\:\mathrm{deduce}? \\ $$$$\left.\mathrm{e}\right)\:\mathrm{Consider}\:\mathrm{another}\:\mathrm{sequence}\:{t}_{{n}} \:\mathrm{defined}\:\mathrm{by} \\ $$$$\:\:\:\:\:\:{t}_{{n}} \:=\:\frac{{u}_{{n}} \:+\:\mathrm{2}{v}_{{n}} }{\mathrm{3}}\:,\:\forall\:{n}\:\in\:\mathbb{N}\: \\ $$$$\mathrm{show}\:\mathrm{that}\:{t}_{{n}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{sequence} \\ $$$$\left.\mathrm{f}\right)\:\mathrm{hence}\:\mathrm{obtain}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sequences}\:\:\left({u}_{{n}} \right)\:\mathrm{and}\:\left({v}_{{n}} \right) \\ $$
Answered by mr W last updated on 29/Dec/19
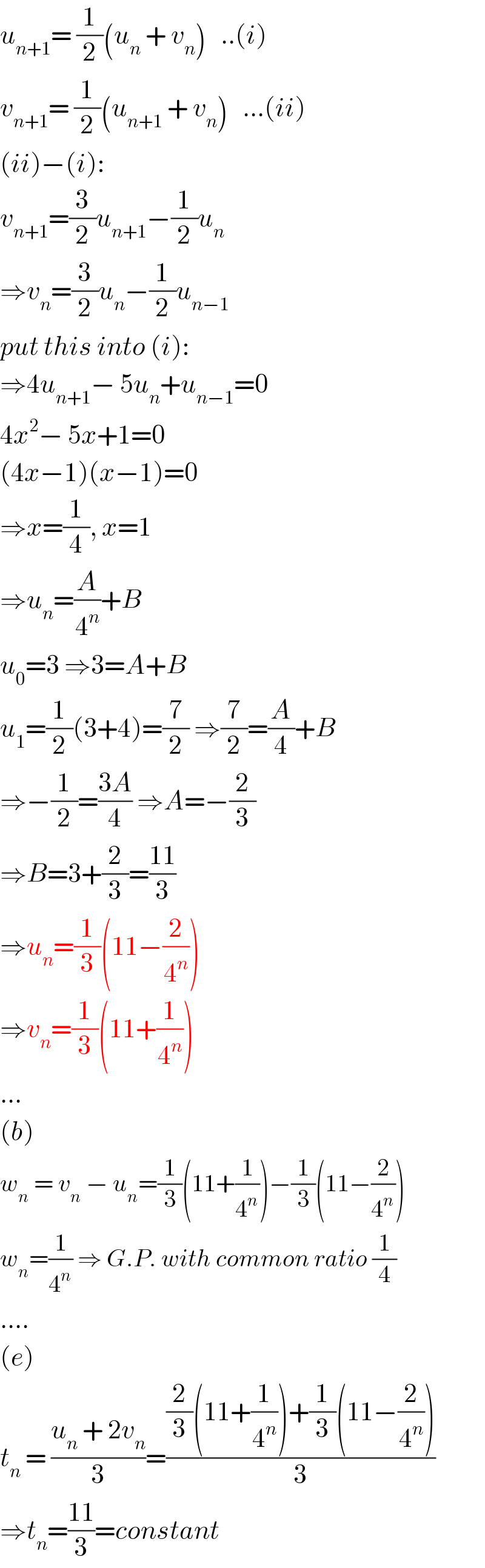
u_(n+1) = (1/2)(u_n + v_n ) ..(i) v_(n+1) = (1/2)(u_(n+1) + v_n ) ...(ii) (ii)−(i): v_(n+1) =(3/2)u_(n+1) −(1/2)u_n ⇒v_n =(3/2)u_n −(1/2)u_(n−1) put this into (i): ⇒4u_(n+1) − 5u_n +u_(n−1) =0 4x^2 − 5x+1=0 (4x−1)(x−1)=0 ⇒x=(1/4), x=1 ⇒u_n =(A/4^n )+B u_0 =3 ⇒3=A+B u_1 =(1/2)(3+4)=(7/2) ⇒(7/2)=(A/4)+B ⇒−(1/2)=((3A)/4) ⇒A=−(2/3) ⇒B=3+(2/3)=((11)/3) ⇒u_n =(1/3)(11−(2/4^n )) ⇒v_n =(1/3)(11+(1/4^n )) ... (b) w_n = v_n − u_n =(1/3)(11+(1/4^n ))−(1/3)(11−(2/4^n )) w_n =(1/4^n ) ⇒ G.P. with common ratio (1/4) .... (e) t_n = ((u_n + 2v_n )/3)=(((2/3)(11+(1/4^n ))+(1/3)(11−(2/4^n )))/3) ⇒t_n =((11)/3)=constant
$${u}_{{n}+\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left({u}_{{n}} \:+\:{v}_{{n}} \right)\:\:\:..\left({i}\right) \\ $$$${v}_{{n}+\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left({u}_{{n}+\mathrm{1}} \:+\:{v}_{{n}} \right)\:\:\:…\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$${v}_{{n}+\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}{u}_{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}} \\ $$$$\Rightarrow{v}_{{n}} =\frac{\mathrm{3}}{\mathrm{2}}{u}_{{n}} −\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}−\mathrm{1}} \\ $$$${put}\:{this}\:{into}\:\left({i}\right): \\ $$$$\Rightarrow\mathrm{4}{u}_{{n}+\mathrm{1}} −\:\mathrm{5}{u}_{{n}} +{u}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\:\mathrm{5}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{4}{x}−\mathrm{1}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{4}},\:{x}=\mathrm{1} \\ $$$$\Rightarrow{u}_{{n}} =\frac{{A}}{\mathrm{4}^{{n}} }+{B} \\ $$$${u}_{\mathrm{0}} =\mathrm{3}\:\Rightarrow\mathrm{3}={A}+{B} \\ $$$${u}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\mathrm{4}\right)=\frac{\mathrm{7}}{\mathrm{2}}\:\Rightarrow\frac{\mathrm{7}}{\mathrm{2}}=\frac{{A}}{\mathrm{4}}+{B} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}{A}}{\mathrm{4}}\:\Rightarrow{A}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{B}=\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{11}}{\mathrm{3}} \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{11}−\frac{\mathrm{2}}{\mathrm{4}^{{n}} }\right) \\ $$$$\Rightarrow{v}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{11}+\frac{\mathrm{1}}{\mathrm{4}^{{n}} }\right) \\ $$$$… \\ $$$$\left({b}\right) \\ $$$${w}_{{n}} \:=\:{v}_{{n}} \:−\:{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{11}+\frac{\mathrm{1}}{\mathrm{4}^{{n}} }\right)−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{11}−\frac{\mathrm{2}}{\mathrm{4}^{{n}} }\right) \\ $$$${w}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}^{{n}} }\:\Rightarrow\:{G}.{P}.\:{with}\:{common}\:{ratio}\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$…. \\ $$$$\left({e}\right) \\ $$$${t}_{{n}} \:=\:\frac{{u}_{{n}} \:+\:\mathrm{2}{v}_{{n}} }{\mathrm{3}}=\frac{\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{11}+\frac{\mathrm{1}}{\mathrm{4}^{{n}} }\right)+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{11}−\frac{\mathrm{2}}{\mathrm{4}^{{n}} }\right)}{\mathrm{3}} \\ $$$$\Rightarrow{t}_{{n}} =\frac{\mathrm{11}}{\mathrm{3}}={constant} \\ $$
Commented by mr W last updated on 29/Dec/19
alternative: ⇒4u_(n+1) − 5u_n +u_(n−1) =0 ⇒4u_(n+1) − 4u_n −(u_n −u_(n−1) )=0 ⇒(u_(n+1) − u_n )=(1/4)(u_n −u_(n−1) ) ⇒c_(n+1) =(1/4)c_n ⇒ G.P. ⇒c_(n+1) =c_1 ((1/4))^n c_1 =u_1 −u_0 =(7/2)−3=(1/2) ⇒c_(n+1) =(1/2)((1/4))^n ⇒u_(n+1) −u_n =(1/2)((1/4))^n ⇒Σ_0 ^n u_(n+1) −Σ_0 ^n u_n =Σ_0 ^n (1/2)((1/4))^n ⇒u_(n+1) −u_0 =(1/2)×((1−((1/4))^(n+1) )/(1−(1/4)))=(2/3)[1−((1/4))^(n+1) ] ⇒u_(n+1) =(2/3)[1−((1/4))^(n+1) ]+3=(1/3)(11−(2/4^(n+1) )) or ⇒u_n =(1/3)(11−(2/4^n ))
$${alternative}: \\ $$$$\Rightarrow\mathrm{4}{u}_{{n}+\mathrm{1}} −\:\mathrm{5}{u}_{{n}} +{u}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}{u}_{{n}+\mathrm{1}} −\:\mathrm{4}{u}_{{n}} −\left({u}_{{n}} −{u}_{{n}−\mathrm{1}} \right)=\mathrm{0} \\ $$$$\Rightarrow\left({u}_{{n}+\mathrm{1}} −\:{u}_{{n}} \right)=\frac{\mathrm{1}}{\mathrm{4}}\left({u}_{{n}} −{u}_{{n}−\mathrm{1}} \right) \\ $$$$\Rightarrow{c}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}{c}_{{n}} \:\:\Rightarrow\:{G}.{P}. \\ $$$$\Rightarrow{c}_{{n}+\mathrm{1}} ={c}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} \\ $$$${c}_{\mathrm{1}} ={u}_{\mathrm{1}} −{u}_{\mathrm{0}} =\frac{\mathrm{7}}{\mathrm{2}}−\mathrm{3}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{c}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} \\ $$$$\Rightarrow{u}_{{n}+\mathrm{1}} −{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} \\ $$$$\Rightarrow\underset{\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{n}+\mathrm{1}} −\underset{\mathrm{0}} {\overset{{n}} {\sum}}{u}_{{n}} =\underset{\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} \\ $$$$\Rightarrow{u}_{{n}+\mathrm{1}} −{u}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}+\mathrm{1}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\mathrm{2}}{\mathrm{3}}\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}+\mathrm{1}} \right] \\ $$$$\Rightarrow{u}_{{n}+\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}+\mathrm{1}} \right]+\mathrm{3}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{11}−\frac{\mathrm{2}}{\mathrm{4}^{{n}+\mathrm{1}} }\right) \\ $$$${or} \\ $$$$\Rightarrow{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{11}−\frac{\mathrm{2}}{\mathrm{4}^{{n}} }\right) \\ $$
Commented by Rio Michael last updated on 29/Dec/19
thanks sir
$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *