Menu Close

u-2i-3j-5k-v-3i-2j-5k-w-2i-3j-k-find-u-v-w-u-v-u-w-

Tinku Tara
Pin




Question Number 225 by 123456 last updated on 25/Jan/15
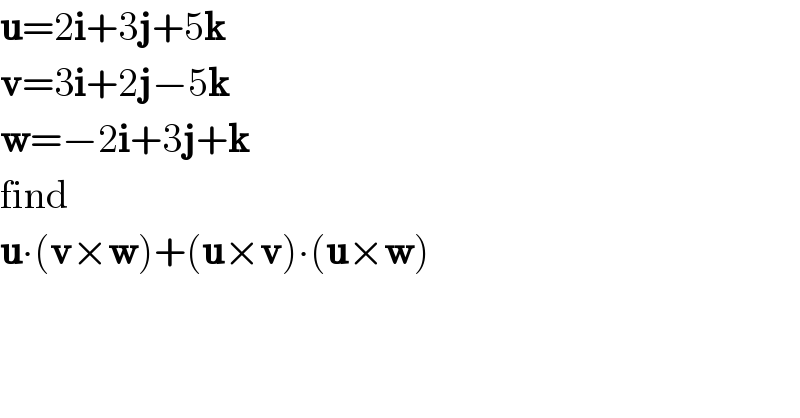
u=2i+3j+5k v=3i+2j−5k w=−2i+3j+k find u∙(v×w)+(u×v)∙(u×w)
$$\boldsymbol{\mathrm{u}}=\mathrm{2}\boldsymbol{\mathrm{i}}+\mathrm{3}\boldsymbol{\mathrm{j}}+\mathrm{5}\boldsymbol{\mathrm{k}} \\ $$$$\boldsymbol{\mathrm{v}}=\mathrm{3}\boldsymbol{\mathrm{i}}+\mathrm{2}\boldsymbol{\mathrm{j}}−\mathrm{5}\boldsymbol{\mathrm{k}} \\ $$$$\boldsymbol{\mathrm{w}}=−\mathrm{2}\boldsymbol{\mathrm{i}}+\mathrm{3}\boldsymbol{\mathrm{j}}+\boldsymbol{\mathrm{k}} \\ $$$$\mathrm{find} \\ $$$$\boldsymbol{\mathrm{u}}\centerdot\left(\boldsymbol{\mathrm{v}}×\boldsymbol{\mathrm{w}}\right)+\left(\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{v}}\right)\centerdot\left(\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{w}}\right) \\ $$
Answered by mreddy last updated on 16/Dec/14
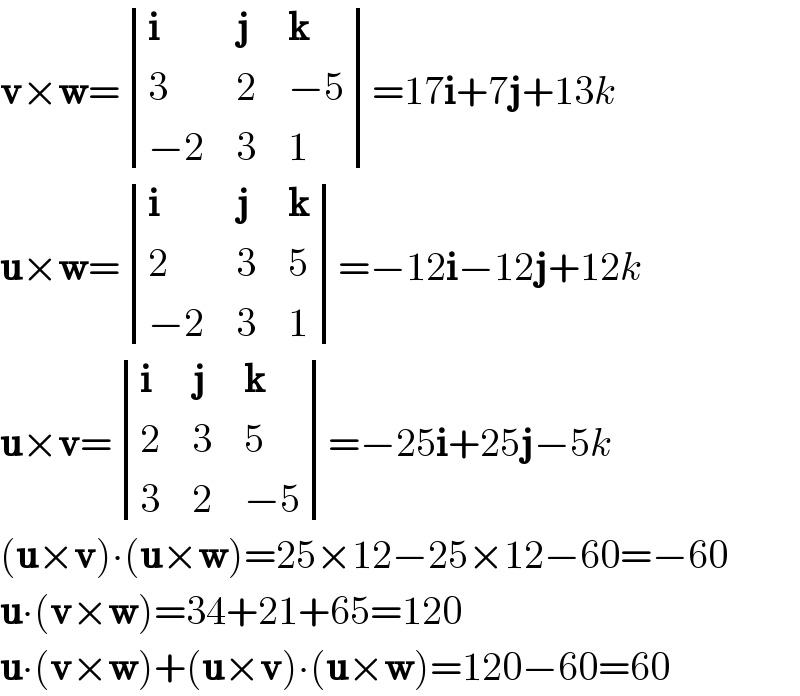
v×w= determinant ((i,j,k),(3,2,(−5)),((−2),3,1))=17i+7j+13k u×w= determinant ((i,j,k),(2,3,5),((−2),3,1))=−12i−12j+12k u×v= determinant ((i,j,k),(2,3,5),(3,2,(−5)))=−25i+25j−5k (u×v)∙(u×w)=25×12−25×12−60=−60 u∙(v×w)=34+21+65=120 u∙(v×w)+(u×v)∙(u×w)=120−60=60
$$\boldsymbol{\mathrm{v}}×\boldsymbol{\mathrm{w}}=\begin{vmatrix}{\boldsymbol{\mathrm{i}}}&{\boldsymbol{\mathrm{j}}}&{\boldsymbol{\mathrm{k}}}\\{\mathrm{3}}&{\mathrm{2}}&{−\mathrm{5}}\\{−\mathrm{2}}&{\mathrm{3}}&{\mathrm{1}}\end{vmatrix}=\mathrm{17}\boldsymbol{\mathrm{i}}+\mathrm{7}\boldsymbol{\mathrm{j}}+\mathrm{13}{k} \\ $$$$\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{w}}=\begin{vmatrix}{\boldsymbol{\mathrm{i}}}&{\boldsymbol{\mathrm{j}}}&{\boldsymbol{\mathrm{k}}}\\{\mathrm{2}}&{\mathrm{3}}&{\mathrm{5}}\\{−\mathrm{2}}&{\mathrm{3}}&{\mathrm{1}}\end{vmatrix}=−\mathrm{12}\boldsymbol{\mathrm{i}}−\mathrm{12}\boldsymbol{\mathrm{j}}+\mathrm{12}{k} \\ $$$$\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{v}}=\begin{vmatrix}{\boldsymbol{\mathrm{i}}}&{\boldsymbol{\mathrm{j}}}&{\boldsymbol{\mathrm{k}}}\\{\mathrm{2}}&{\mathrm{3}}&{\mathrm{5}}\\{\mathrm{3}}&{\mathrm{2}}&{−\mathrm{5}}\end{vmatrix}=−\mathrm{25}\boldsymbol{\mathrm{i}}+\mathrm{25}\boldsymbol{\mathrm{j}}−\mathrm{5}{k} \\ $$$$\left(\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{v}}\right)\centerdot\left(\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{w}}\right)=\mathrm{25}×\mathrm{12}−\mathrm{25}×\mathrm{12}−\mathrm{60}=−\mathrm{60} \\ $$$$\boldsymbol{\mathrm{u}}\centerdot\left(\boldsymbol{\mathrm{v}}×\boldsymbol{\mathrm{w}}\right)=\mathrm{34}+\mathrm{21}+\mathrm{65}=\mathrm{120} \\ $$$$\boldsymbol{\mathrm{u}}\centerdot\left(\boldsymbol{\mathrm{v}}×\boldsymbol{\mathrm{w}}\right)+\left(\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{v}}\right)\centerdot\left(\boldsymbol{\mathrm{u}}×\boldsymbol{\mathrm{w}}\right)=\mathrm{120}−\mathrm{60}=\mathrm{60} \\ $$

Pin