Question Number 75593 by ajfour last updated on 13/Dec/19
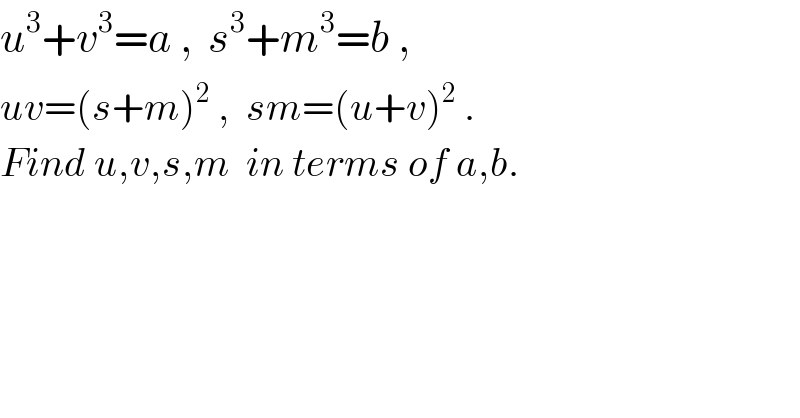
$${u}^{\mathrm{3}} +{v}^{\mathrm{3}} ={a}\:,\:\:{s}^{\mathrm{3}} +{m}^{\mathrm{3}} ={b}\:, \\ $$$${uv}=\left({s}+{m}\right)^{\mathrm{2}} \:,\:\:{sm}=\left({u}+{v}\right)^{\mathrm{2}} \:. \\ $$$${Find}\:{u},{v},{s},{m}\:\:{in}\:{terms}\:{of}\:{a},{b}. \\ $$
Answered by behi83417@gmail.com last updated on 13/Dec/19
![(s+m)[(s+m)^2 −3sm]=b⇒ uv[uv−3(u+v)^2 ]^2 =b^2 (u+v)[(u+v)^2 −3uv]=a ⇒_(uv=q) ^(u+v=p) { ((q(q−3p^2 )^2 =b^2 )),((p(p^2 −3q)=a)) :} ⇒ { ((q^3 −6q^2 p^2 +9qp^4 =b^2 )),((p^3 −3pq=a⇒q=((p^3 −a)/(3p)))) :} ⇒(((p^3 −a)^3 )/(27p^3 ))−6p^2 (((p^3 −a)^2 )/(9p^2 ))+9p^4 ((p^3 −a)/(3p))=b^2 ⇒(p^3 −a)^3 −18p^3 (p^3 −a)^2 +81p^6 (p^3 −a)=27p^3 b^2 ⇒^(p^3 =t) (t−a)^3 −18t(t−a)^2 +81t^2 (t−a)=27tb^2 ⇒(t^3 −3at^2 +3a^2 t−a^3 )−18t(t^2 −2at+a^2 )+81t^2 (t−a)=27tb^2 ⇒64t^3 −48at^2 −(15a^2 +27b^2 )t−a^3 =0 ⇒t^3 −(3/4)at^2 −(3/(64))(5a^2 +9b^2 )t−(a^3 /(64))=0 ⇒^(T=t+(a/4)) T^3 −(3/(64))(17a^2 +9b^2 )T−(3/(256))(4a^3 +5a^2 +9b^2 )=0 △=−3×((−3)/(256))(4a^3 +5a^2 +9b^2 )>0 k=((−27×((−3)/(256))(4a^3 +5a^2 +9b^2 ))/(2×(9/(256))(4a^3 +5a^2 +9b^2 )(√((9/(256))(4a^3 +5a^2 +9b^2 )))))<1 T_1 =((√(4a^3 +5a^2 +9b^2 ))/8)×cos((1/3)cos^(−1) ((24)/( (√(4a^3 +5a^2 +9b^2 ))))) T_2 =((√(4a^3 +5a^2 +9b^2 ))/8)×cos((1/3)cos^(−1) ((24)/( (√(4a^3 +5a^2 +9b^2 ))))−((2π)/3)) T_3 =((√(4a^3 +5a^2 +9b^2 ))/8)×cos((1/3)cos^(−1) ((24)/( (√(4a^3 +5a^2 +9b^2 ))))+((2π)/3)) p_i ^3 =t_i =^(i=1,2,3) T_i −(a/4)=((√(4a^3 +5a^2 +9b^2 ))/8)cos((1/3)cos^(−1) ((24)/( (√(4a^3 +5a^2 +9b^2 )))))−(a/4) ⇒p_1 =((((√(4a^3 +5a^2 +9b^2 ))/8)cos((1/3)cos^(−1) ((24)/( (√(4a^3 +5a^2 +9b^2 )))))−(a/4)))^(1/3) q_1 =((p^3 −a)/(3p))=((((√(4a^3 +5a^2 +9b^2 ))/8)cos((1/3)cos^(−1) ((24)/( (√(4a^3 +5a^2 +9b^2 )))))−((5a)/4))/(3((((√(4a^3 +5a^2 +9b^2 ))/8)cos((1/3)cos^(−1) ((24)/( (√(4a^3 +5a^2 +9b^2 )))))−(a/4)))^(1/3) )) u=−(p/2)+((√(p^2 −4q))/2),v=−(p/2)−((√(p^2 −4q))/2) s=−((uv)/2)+((√(uv−4(u+v)^2 ))/2) m=−((uv)/2)−((√(uv−4(u+v)^2 ))/2)](https://www.tinkutara.com/question/Q75610.png)
$$\left(\mathrm{s}+\mathrm{m}\right)\left[\left(\mathrm{s}+\mathrm{m}\right)^{\mathrm{2}} −\mathrm{3sm}\right]=\mathrm{b}\Rightarrow \\ $$$$\mathrm{uv}\left[\mathrm{uv}−\mathrm{3}\left(\mathrm{u}+\mathrm{v}\right)^{\mathrm{2}} \right]^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} \\ $$$$\left(\mathrm{u}+\mathrm{v}\right)\left[\left(\mathrm{u}+\mathrm{v}\right)^{\mathrm{2}} −\mathrm{3uv}\right]=\mathrm{a} \\ $$$$\underset{\mathrm{uv}=\mathrm{q}} {\overset{\mathrm{u}+\mathrm{v}=\mathrm{p}} {\Rightarrow}}\:\:\begin{cases}{\mathrm{q}\left(\mathrm{q}−\mathrm{3p}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} }\\{\mathrm{p}\left(\mathrm{p}^{\mathrm{2}} −\mathrm{3q}\right)=\mathrm{a}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{q}^{\mathrm{3}} −\mathrm{6q}^{\mathrm{2}} \mathrm{p}^{\mathrm{2}} +\mathrm{9qp}^{\mathrm{4}} =\mathrm{b}^{\mathrm{2}} }\\{\mathrm{p}^{\mathrm{3}} −\mathrm{3pq}=\mathrm{a}\Rightarrow\mathrm{q}=\frac{\mathrm{p}^{\mathrm{3}} −\mathrm{a}}{\mathrm{3p}}}\end{cases} \\ $$$$\Rightarrow\frac{\left(\mathrm{p}^{\mathrm{3}} −\mathrm{a}\right)^{\mathrm{3}} }{\mathrm{27p}^{\mathrm{3}} }−\mathrm{6p}^{\mathrm{2}} \frac{\left(\mathrm{p}^{\mathrm{3}} −\mathrm{a}\right)^{\mathrm{2}} }{\mathrm{9p}^{\mathrm{2}} }+\mathrm{9p}^{\mathrm{4}} \:\frac{\mathrm{p}^{\mathrm{3}} −\mathrm{a}}{\mathrm{3p}}=\mathrm{b}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{p}^{\mathrm{3}} −\mathrm{a}\right)^{\mathrm{3}} −\mathrm{18p}^{\mathrm{3}} \left(\mathrm{p}^{\mathrm{3}} −\mathrm{a}\right)^{\mathrm{2}} +\mathrm{81p}^{\mathrm{6}} \left(\mathrm{p}^{\mathrm{3}} −\mathrm{a}\right)=\mathrm{27p}^{\mathrm{3}} \mathrm{b}^{\mathrm{2}} \\ $$$$\overset{\mathrm{p}^{\mathrm{3}} =\mathrm{t}} {\Rightarrow}\left(\mathrm{t}−\mathrm{a}\right)^{\mathrm{3}} −\mathrm{18t}\left(\mathrm{t}−\mathrm{a}\right)^{\mathrm{2}} +\mathrm{81t}^{\mathrm{2}} \left(\mathrm{t}−\mathrm{a}\right)=\mathrm{27tb}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{t}^{\mathrm{3}} −\mathrm{3at}^{\mathrm{2}} +\mathrm{3a}^{\mathrm{2}} \mathrm{t}−\mathrm{a}^{\mathrm{3}} \right)−\mathrm{18t}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2at}+\mathrm{a}^{\mathrm{2}} \right)+\mathrm{81t}^{\mathrm{2}} \left(\mathrm{t}−\mathrm{a}\right)=\mathrm{27tb}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{64t}^{\mathrm{3}} −\mathrm{48at}^{\mathrm{2}} −\left(\mathrm{15a}^{\mathrm{2}} +\mathrm{27b}^{\mathrm{2}} \right)\mathrm{t}−\mathrm{a}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{t}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{4}}\mathrm{at}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{64}}\left(\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} \right)\mathrm{t}−\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{64}}=\mathrm{0} \\ $$$$\overset{\mathrm{T}=\mathrm{t}+\frac{\mathrm{a}}{\mathrm{4}}} {\Rightarrow}\mathrm{T}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{64}}\left(\mathrm{17a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} \right)\mathrm{T}−\frac{\mathrm{3}}{\mathrm{256}}\left(\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\bigtriangleup=−\mathrm{3}×\frac{−\mathrm{3}}{\mathrm{256}}\left(\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} \right)>\mathrm{0} \\ $$$$\mathrm{k}=\frac{−\mathrm{27}×\frac{−\mathrm{3}}{\mathrm{256}}\left(\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} \right)}{\mathrm{2}×\frac{\mathrm{9}}{\mathrm{256}}\left(\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} \right)\sqrt{\frac{\mathrm{9}}{\mathrm{256}}\left(\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} \right)}}<\mathrm{1} \\ $$$$\mathrm{T}_{\mathrm{1}} =\frac{\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}{\mathrm{8}}×\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\:\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{T}_{\mathrm{2}} =\frac{\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}{\mathrm{8}}×\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\:\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}−\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{T}_{\mathrm{3}} =\frac{\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}{\mathrm{8}}×\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\:\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{p}_{\mathrm{i}} ^{\mathrm{3}} =\mathrm{t}_{\mathrm{i}} \overset{\mathrm{i}=\mathrm{1},\mathrm{2},\mathrm{3}} {=}\mathrm{T}_{\mathrm{i}} −\frac{\mathrm{a}}{\mathrm{4}}=\frac{\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}{\mathrm{8}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\:\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}\right)−\frac{\mathrm{a}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{p}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}{\mathrm{8}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\:\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}\right)−\frac{\mathrm{a}}{\mathrm{4}}} \\ $$$$\mathrm{q}_{\mathrm{1}} =\frac{\mathrm{p}^{\mathrm{3}} −\mathrm{a}}{\mathrm{3p}}=\frac{\frac{\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}{\mathrm{8}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\:\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}\right)−\frac{\mathrm{5a}}{\mathrm{4}}}{\mathrm{3}\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}{\mathrm{8}}\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{24}}{\:\sqrt{\mathrm{4a}^{\mathrm{3}} +\mathrm{5a}^{\mathrm{2}} +\mathrm{9b}^{\mathrm{2}} }}\right)−\frac{\mathrm{a}}{\mathrm{4}}}} \\ $$$$\boldsymbol{\mathrm{u}}=−\frac{\boldsymbol{\mathrm{p}}}{\mathrm{2}}+\frac{\sqrt{\boldsymbol{\mathrm{p}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{q}}}}{\mathrm{2}},\boldsymbol{\mathrm{v}}=−\frac{\boldsymbol{\mathrm{p}}}{\mathrm{2}}−\frac{\sqrt{\boldsymbol{\mathrm{p}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{q}}}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{s}}=−\frac{\boldsymbol{\mathrm{uv}}}{\mathrm{2}}+\frac{\sqrt{\boldsymbol{\mathrm{uv}}−\mathrm{4}\left(\boldsymbol{\mathrm{u}}+\boldsymbol{\mathrm{v}}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{m}}=−\frac{\boldsymbol{\mathrm{uv}}}{\mathrm{2}}−\frac{\sqrt{\boldsymbol{\mathrm{uv}}−\mathrm{4}\left(\boldsymbol{\mathrm{u}}+\boldsymbol{\mathrm{v}}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$
