Question Number 74026 by mathmax by abdo last updated on 17/Nov/19

$${U}_{{n}} {is}\:{a}\:{sequence}\:{wich}\:{verfy}\: \\ $$$$\forall{n}\:\in{N}\:\:\:\:\:\:\:\:\mathrm{2}^{{n}} \left(\:{U}_{{n}} +{U}_{{n}+\mathrm{1}} \right)=\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{U}_{{n}} \:{interms}\:{of}\:{n} \\ $$$$\left.\mathrm{2}\right)\:{is}\:\left({U}_{{n}} \right)\:{cojverhent}\:? \\ $$
Commented by mathmax by abdo last updated on 18/Nov/19
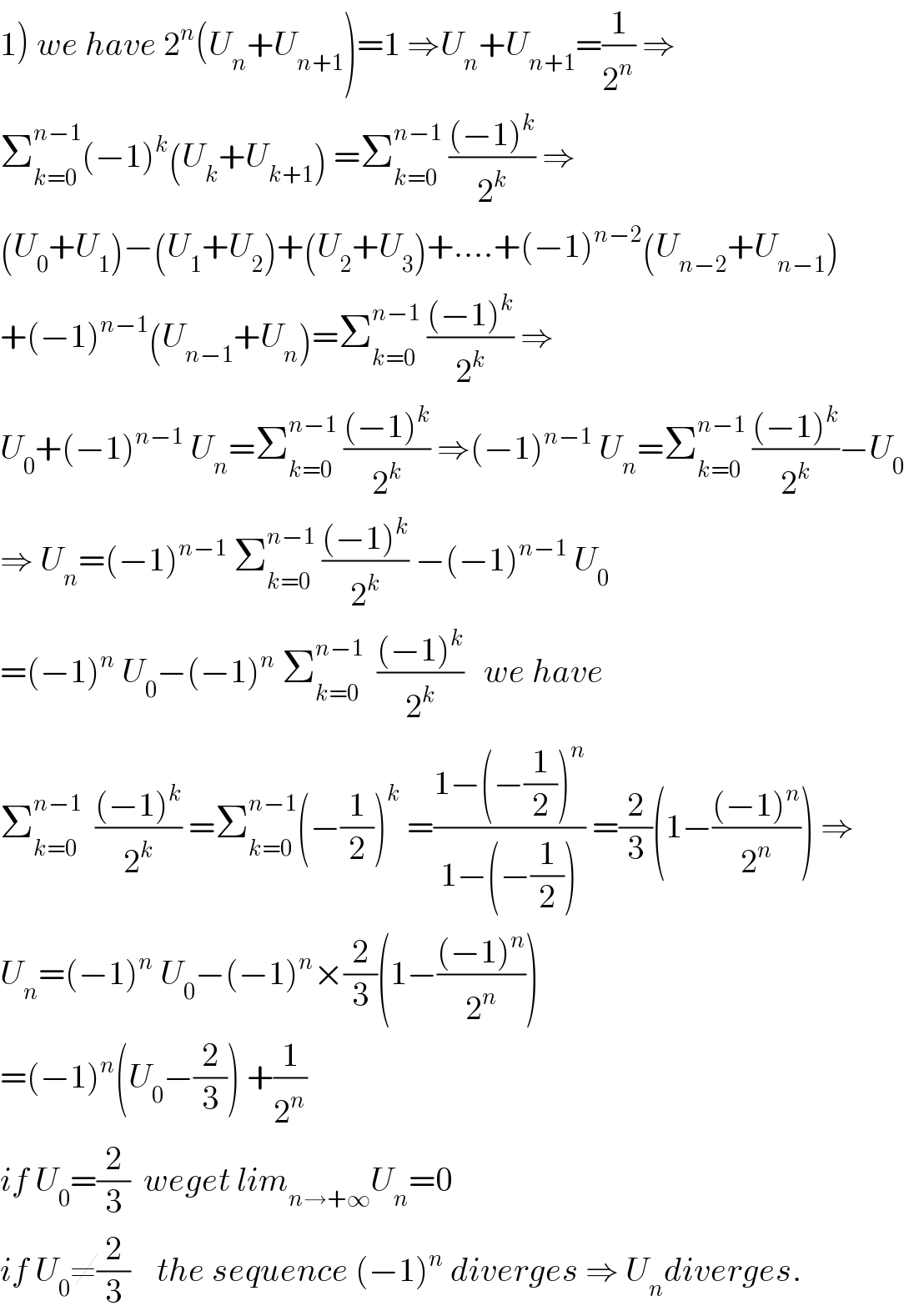
$$\left.\mathrm{1}\right)\:{we}\:{have}\:\mathrm{2}^{{n}} \left({U}_{{n}} +{U}_{{n}+\mathrm{1}} \right)=\mathrm{1}\:\Rightarrow{U}_{{n}} +{U}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} \left({U}_{{k}} +{U}_{{k}+\mathrm{1}} \right)\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\:\Rightarrow \\ $$$$\left({U}_{\mathrm{0}} +{U}_{\mathrm{1}} \right)−\left({U}_{\mathrm{1}} +{U}_{\mathrm{2}} \right)+\left({U}_{\mathrm{2}} +{U}_{\mathrm{3}} \right)+….+\left(−\mathrm{1}\right)^{{n}−\mathrm{2}} \left({U}_{{n}−\mathrm{2}} +{U}_{{n}−\mathrm{1}} \right) \\ $$$$+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({U}_{{n}−\mathrm{1}} +{U}_{{n}} \right)=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\:\Rightarrow \\ $$$${U}_{\mathrm{0}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\:\Rightarrow\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }−{U}_{\mathrm{0}} \\ $$$$\Rightarrow\:{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\:−\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{U}_{\mathrm{0}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:{U}_{\mathrm{0}} −\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\:\:\:{we}\:{have} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}} \:=\frac{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} }{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\right)\:\Rightarrow \\ $$$${U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \:{U}_{\mathrm{0}} −\left(−\mathrm{1}\right)^{{n}} ×\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\right) \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \left({U}_{\mathrm{0}} −\frac{\mathrm{2}}{\mathrm{3}}\right)\:+\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${if}\:{U}_{\mathrm{0}} =\frac{\mathrm{2}}{\mathrm{3}}\:\:{weget}\:{lim}_{{n}\rightarrow+\infty} {U}_{{n}} =\mathrm{0} \\ $$$${if}\:{U}_{\mathrm{0}} \neq\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:{the}\:{sequence}\:\left(−\mathrm{1}\right)^{{n}} \:{diverges}\:\Rightarrow\:{U}_{{n}} {diverges}. \\ $$
Commented by abdomathmax last updated on 17/Nov/19
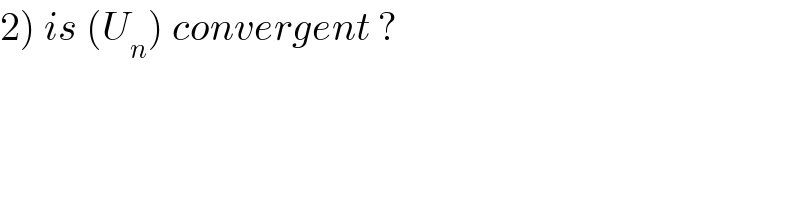
$$\left.\mathrm{2}\right)\:{is}\:\left({U}_{{n}} \right)\:{convergent}\:? \\ $$
Commented by mathmax by abdo last updated on 18/Nov/19
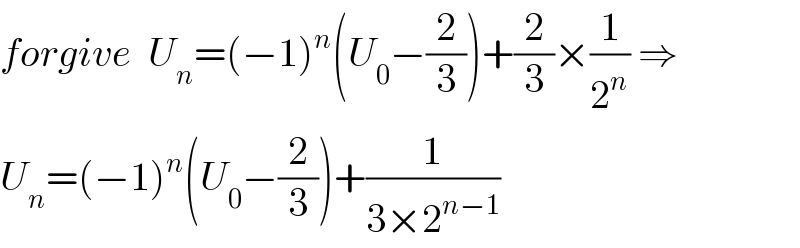
$${forgive}\:\:{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \left({U}_{\mathrm{0}} −\frac{\mathrm{2}}{\mathrm{3}}\right)+\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\Rightarrow \\ $$$${U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \left({U}_{\mathrm{0}} −\frac{\mathrm{2}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{2}^{{n}−\mathrm{1}} } \\ $$
Commented by mathmax by abdo last updated on 18/Nov/19

$${all}\:{answers}\:{given}\:{are}\:{correct}\:{sometimes}\:{with}\:{a}\:{small}\:{eroor}\:{of} \\ $$$${typo}\:\:{and}\:{when}\:{i}\:{find}\:{a}\:{big}\:{mistake}\:{i}\:{delet}\:{the}\:{post}\:{and}\:{send} \\ $$$${another}… \\ $$
Commented by Joel578 last updated on 18/Nov/19

$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{would}\:\mathrm{be}\:\mathrm{better}\:\mathrm{if}\:\mathrm{you}\:\mathrm{use} \\ $$$$'{edit}\:{post}'\:\mathrm{feature},\:\mathrm{so}\:\mathrm{others}\:\mathrm{can}\:\mathrm{see}\:\mathrm{the}\:\mathrm{correct} \\ $$$$\mathrm{question}/\mathrm{answer}\:\:\mathrm{directly} \\ $$
Answered by mind is power last updated on 18/Nov/19
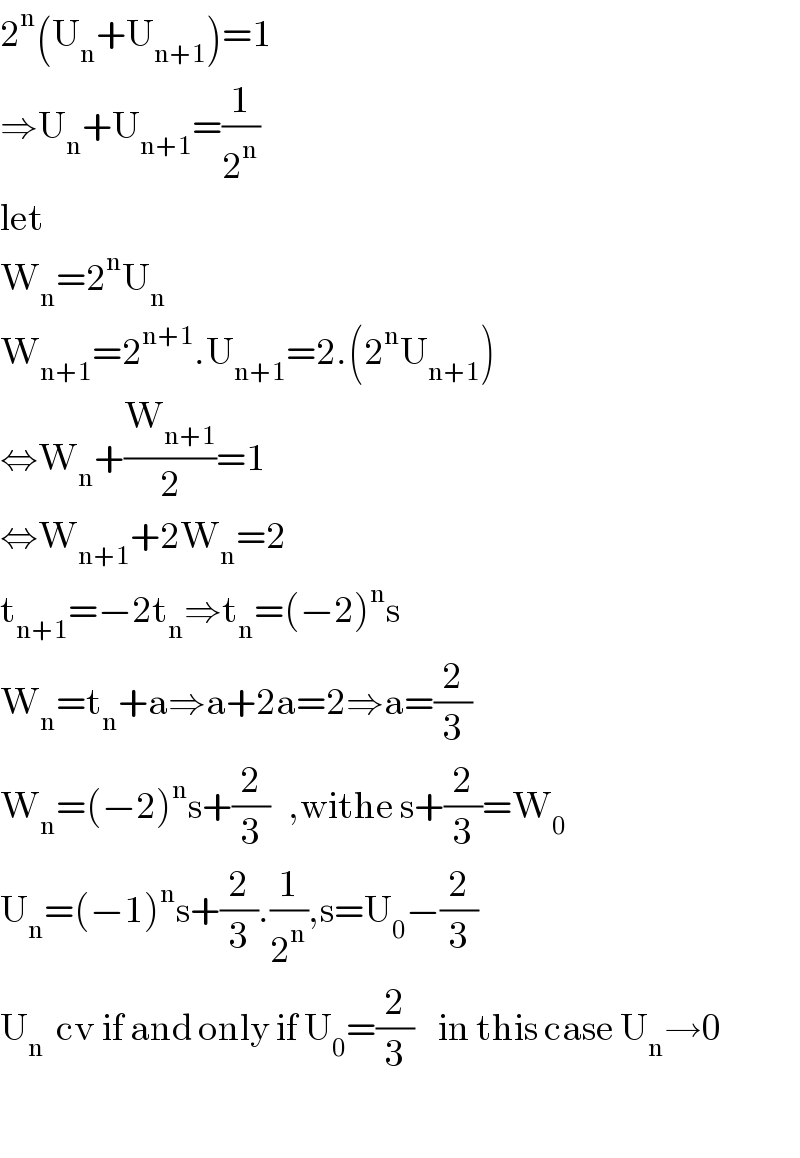
$$\mathrm{2}^{\mathrm{n}} \left(\mathrm{U}_{\mathrm{n}} +\mathrm{U}_{\mathrm{n}+\mathrm{1}} \right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}} +\mathrm{U}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} } \\ $$$$\mathrm{let} \\ $$$$\mathrm{W}_{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \mathrm{U}_{\mathrm{n}} \\ $$$$\mathrm{W}_{\mathrm{n}+\mathrm{1}} =\mathrm{2}^{\mathrm{n}+\mathrm{1}} .\mathrm{U}_{\mathrm{n}+\mathrm{1}} =\mathrm{2}.\left(\mathrm{2}^{\mathrm{n}} \mathrm{U}_{\mathrm{n}+\mathrm{1}} \right) \\ $$$$\Leftrightarrow\mathrm{W}_{\mathrm{n}} +\frac{\mathrm{W}_{\mathrm{n}+\mathrm{1}} }{\mathrm{2}}=\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{W}_{\mathrm{n}+\mathrm{1}} +\mathrm{2W}_{\mathrm{n}} =\mathrm{2} \\ $$$$\mathrm{t}_{\mathrm{n}+\mathrm{1}} =−\mathrm{2t}_{\mathrm{n}} \Rightarrow\mathrm{t}_{\mathrm{n}} =\left(−\mathrm{2}\right)^{\mathrm{n}} \mathrm{s} \\ $$$$\mathrm{W}_{\mathrm{n}} =\mathrm{t}_{\mathrm{n}} +\mathrm{a}\Rightarrow\mathrm{a}+\mathrm{2a}=\mathrm{2}\Rightarrow\mathrm{a}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{W}_{\mathrm{n}} =\left(−\mathrm{2}\right)^{\mathrm{n}} \mathrm{s}+\frac{\mathrm{2}}{\mathrm{3}}\:\:\:,\mathrm{withe}\:\mathrm{s}+\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{W}_{\mathrm{0}} \\ $$$$\mathrm{U}_{\mathrm{n}} =\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{s}+\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} },\mathrm{s}=\mathrm{U}_{\mathrm{0}} −\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{U}_{\mathrm{n}} \:\:\mathrm{cv}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{U}_{\mathrm{0}} =\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{U}_{\mathrm{n}} \rightarrow\mathrm{0} \\ $$$$ \\ $$
