Menu Close

U-n-isa-sequence-woch-verify-U-n-U-n-1-n-2-1-n-n-0-1-detdrmine-U-n-interm-of-n-2-find-nsture-of-the-serie-U-n-n-4-3-calculate-k-j-n-U-k-U-j-

Tinku Tara 0 Comments
Pin




Question Number 77754 by abdomathmax last updated on 09/Jan/20
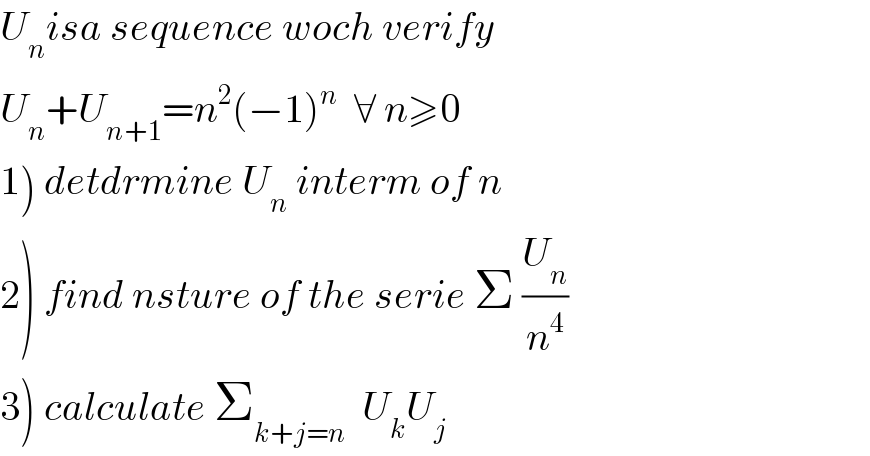
U_n isa sequence woch verify U_n +U_(n+1) =n^2 (−1)^n ∀ n≥0 1) detdrmine U_n interm of n 2) find nsture of the serie Σ (U_n /n^4 ) 3) calculate Σ_(k+j=n) U_k U_j
$${U}_{{n}} {isa}\:{sequence}\:{woch}\:{verify} \\ $$$${U}_{{n}} +{U}_{{n}+\mathrm{1}} ={n}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{n}} \:\:\forall\:{n}\geqslant\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{detdrmine}\:{U}_{{n}} \:{interm}\:{of}\:{n} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{nsture}\:{of}\:{the}\:{serie}\:\Sigma\:\frac{{U}_{{n}} }{{n}^{\mathrm{4}} } \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\sum_{{k}+{j}={n}} \:\:{U}_{{k}} {U}_{{j}} \\ $$
Commented by mathmax by abdo last updated on 10/Jan/20
we have U_n +U_(n+1) =n^2 (−1)^n ⇒ Σ_(k=0) ^(n−1) (−1)^k (U_k +U_(k+1) ) =Σ_(k=0) ^(n−1) (−1)^k k^2 ⇒ U_0 +U_1 −(U_1 +U_2 )+....(−1)^(n−2) (U_(n−2) +U_(n−1) )+(−1)^(n−1) (U_(n−1) +U_n ) Σ_(k=0) ^(n−1) k^2 (−1)^k ⇒ U_0 +(−1)^(n−1) U_n =Σ_(k=0) ^(n−1) k^2 (−1)^k ⇒ (−1)^(n−1) U_n =Σ_(k=0) ^(n−1) k^2 (−1)^k −U_0 ⇒ U_n =(−1)^(n−1) Σ_(k=0) ^(n−1) k^2 (−1)^k −(−1)^(n−1) U_0 =(−1)^n U_0 −(−1)^n Σ_(k=0) ^(n−1) k^2 (−1)^k let p(x)= 1+x +x^2 +...+x^(n−1) =Σ_(k=0) ^(n−1) x^k ⇒p(x)=((x^n −1)/(x−1)) (x≠1) ⇒Σ_(k=1) ^(n−1) k x^(k−1) =((nx^(n−1) (x−1)−(x^n −1)×1)/((x−1)^2 ))= =((nx^n −nx^(n−1) −x^n +1)/((x−1)^2 )) =(((n−1)x^n −nx^(n−1) +1)/((x−1)^2 )) ⇒ Σ_(k=0) ^(n−1) k x^k =(x/((x−1)^2 )){(n−1)x^n −nx^(n−1) +1}=λ(x) ⇒ Σ_(k=1) ^(n−1) k^2 x^(k−1) =λ^′ (x) ⇒Σ_(k=0) ^(n−1) k^2 x^k =xλ^′ (x) ⇒ Σ_(k=0) ^(n−1) k^2 (−1)^k =−λ^′ (−1) ⇒ U_n =(−1)^n U_o +(−1)^n λ^′ (−1) we have λ(x)=(((n−1)x^(n+1) −nx^n +x)/((x−1)^2 )) ⇒ λ^′ (x) =(({ (n^2 −1)x^n −n^2 x^(n−1) +1)(x−1)^2 −2(x−1){(n−1)x^(n+1) −nx^n +x})/((x−1)^4 )) =(((x−1){ (n^2 −1)x^n −n^2 x^(n−1) +1}−2{(n−1)x^(n+1) −nx^n +1})/((x−1)^3 )) ⇒ λ^′ (−1) =(((−2){(n^2 −1)(−1)^n −n^2 (−1)^(n−1) +1}−2{(n−1)(−1)^(n+1) −n(−1)^n +1})/(−8)) =(((2n^2 −1)(−1)^n +1−2{(−2n+1)(−1)^n +1})/4) =(((2n^2 +4n−3)(−1)^n −1)/4) ⇒ U_n =(−1)^n U_0 +(−1)^n ×((−1+(2n^2 +4n−3)(−1)^n )/4) for n≥1
$${we}\:{have}\:{U}_{{n}} +{U}_{{n}+\mathrm{1}} ={n}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{n}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left(−\mathrm{1}\right)^{{k}} \left({U}_{{k}} +{U}_{{k}+\mathrm{1}} \right)\:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(−\mathrm{1}\right)^{{k}} \:{k}^{\mathrm{2}} \:\Rightarrow \\ $$$${U}_{\mathrm{0}} +{U}_{\mathrm{1}} −\left({U}_{\mathrm{1}} +{U}_{\mathrm{2}} \right)+….\left(−\mathrm{1}\right)^{{n}−\mathrm{2}} \left({U}_{{n}−\mathrm{2}} +{U}_{{n}−\mathrm{1}} \right)+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({U}_{{n}−\mathrm{1}} +{U}_{{n}} \right) \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:\Rightarrow\:{U}_{\mathrm{0}} \:+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:\Rightarrow \\ $$$$\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {U}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} −{U}_{\mathrm{0}} \:\Rightarrow \\ $$$${U}_{{n}} =\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} −\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{U}_{\mathrm{0}} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \:{U}_{\mathrm{0}} −\left(−\mathrm{1}\right)^{{n}} \:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \\ $$$${let}\:{p}\left({x}\right)=\:\mathrm{1}+{x}\:+{x}^{\mathrm{2}} \:+…+{x}^{{n}−\mathrm{1}} \:=\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{x}^{{k}} \:\Rightarrow{p}\left({x}\right)=\frac{{x}^{{n}} −\mathrm{1}}{{x}−\mathrm{1}}\:\:\left({x}\neq\mathrm{1}\right) \\ $$$$\Rightarrow\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{k}\:{x}^{{k}−\mathrm{1}} =\frac{{nx}^{{n}−\mathrm{1}} \left({x}−\mathrm{1}\right)−\left({x}^{{n}} −\mathrm{1}\right)×\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\frac{{nx}^{{n}} −{nx}^{{n}−\mathrm{1}} −{x}^{{n}} \:+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\left({n}−\mathrm{1}\right){x}^{{n}} −{nx}^{{n}−\mathrm{1}} \:+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:{x}^{{k}} =\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\left\{\left({n}−\mathrm{1}\right){x}^{{n}} −{nx}^{{n}−\mathrm{1}} +\mathrm{1}\right\}=\lambda\left({x}\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {k}^{\mathrm{2}} {x}^{{k}−\mathrm{1}} \:=\lambda^{'} \left({x}\right)\:\Rightarrow\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}^{\mathrm{2}} \:{x}^{{k}} \:={x}\lambda^{'} \left({x}\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:=−\lambda^{'} \left(−\mathrm{1}\right)\:\Rightarrow \\ $$$${U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \:{U}_{{o}} +\left(−\mathrm{1}\right)^{{n}} \:\lambda^{'} \left(−\mathrm{1}\right)\:\:\:{we}\:{have}\: \\ $$$$\lambda\left({x}\right)=\frac{\left({n}−\mathrm{1}\right){x}^{{n}+\mathrm{1}} −{nx}^{{n}} \:+{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\lambda^{'} \left({x}\right)\:=\frac{\left\{\:\:\left({n}^{\mathrm{2}} −\mathrm{1}\right){x}^{{n}} −{n}^{\mathrm{2}} \:{x}^{{n}−\mathrm{1}} \:+\mathrm{1}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left({x}−\mathrm{1}\right)\left\{\left({n}−\mathrm{1}\right){x}^{{n}+\mathrm{1}} −{nx}^{{n}} \:+{x}\right\}}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\frac{\left({x}−\mathrm{1}\right)\left\{\:\left({n}^{\mathrm{2}} −\mathrm{1}\right){x}^{{n}} −{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} +\mathrm{1}\right\}−\mathrm{2}\left\{\left({n}−\mathrm{1}\right){x}^{{n}+\mathrm{1}} −{nx}^{{n}} \:+\mathrm{1}\right\}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\lambda^{'} \left(−\mathrm{1}\right)\:=\frac{\left(−\mathrm{2}\right)\left\{\left({n}^{\mathrm{2}} −\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} −{n}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} +\mathrm{1}\right\}−\mathrm{2}\left\{\left({n}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −{n}\left(−\mathrm{1}\right)^{{n}} \:+\mathrm{1}\right\}}{−\mathrm{8}} \\ $$$$=\frac{\left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \:+\mathrm{1}−\mathrm{2}\left\{\left(−\mathrm{2}{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \:+\mathrm{1}\right\}}{\mathrm{4}} \\ $$$$=\frac{\left(\mathrm{2}{n}^{\mathrm{2}} \:+\mathrm{4}{n}−\mathrm{3}\right)\left(−\mathrm{1}\right)^{{n}} \:−\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \:{U}_{\mathrm{0}} \:\:+\left(−\mathrm{1}\right)^{{n}} ×\frac{−\mathrm{1}+\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{3}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}}\:{for}\:{n}\geqslant\mathrm{1} \\ $$
Commented by mr W last updated on 10/Jan/20
please check sir: if U_n =(−1)^n U_0 +(−1)^n ×((−1+(2n^2 +4n−3)(−1)^n )/4) U_(n+1) =(−1)^(n+1) U_0 +(−1)^(n+1) ×((−1+[2(n+1)^2 +4(n+1)−3](−1)^(n+1) )/4) U_(n+1) =−(−1)^n U_0 +(−1)^n ×((1+[2n^2 +8n+3](−1)^n )/4) ⇒U_(n+1) +U_n = (−1)^(2n) (n^2 +3n)≠(−1)^n n^2
$${please}\:{check}\:{sir}: \\ $$$${if}\:{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \:{U}_{\mathrm{0}} \:\:+\left(−\mathrm{1}\right)^{{n}} ×\frac{−\mathrm{1}+\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{3}\right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}} \\ $$$${U}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:{U}_{\mathrm{0}} \:\:+\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} ×\frac{−\mathrm{1}+\left[\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\left({n}+\mathrm{1}\right)−\mathrm{3}\right]\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{4}} \\ $$$${U}_{{n}+\mathrm{1}} =−\left(−\mathrm{1}\right)^{{n}} \:{U}_{\mathrm{0}} \:\:+\left(−\mathrm{1}\right)^{{n}} ×\frac{\mathrm{1}+\left[\mathrm{2}{n}^{\mathrm{2}} +\mathrm{8}{n}+\mathrm{3}\right]\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}} \\ $$$$\Rightarrow{U}_{{n}+\mathrm{1}} +{U}_{{n}} =\:\left(−\mathrm{1}\right)^{\mathrm{2}{n}} \left({n}^{\mathrm{2}} +\mathrm{3}{n}\right)\neq\left(−\mathrm{1}\right)^{{n}} {n}^{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 11/Jan/20
perhaps my answer contain a error of calculus but sir mrw give opportonity to the method...
$${perhaps}\:{my}\:{answer}\:{contain}\:{a}\:{error}\:{of}\:{calculus}\:{but}\:{sir}\:{mrw} \\ $$$${give}\:{opportonity}\:{to}\:{the}\:{method}… \\ $$
Answered by mr W last updated on 10/Jan/20
say U_n =V_n +(−1)^(n−1) [an^3 +bn^2 +cn] U_(n+1) =V_(n+1) +(−1)^n [a(n+1)^3 +b(n+1)^2 +c(n+1)] U_(n+1) +U_n =V_(n+1) +V_n +(−1)^n {a[−n^3 +(n+1)^3 ]+b[−n^2 +(n+1)^2 ]+c[−n+(n+1)]} U_(n+1) +U_n =V_(n+1) +V_n +(−1)^n {a[3n^2 +3n+1]+b[2n+1]+c} U_(n+1) +U_n =V_(n+1) +V_n +(−1)^n {3an^2 +(3a+2b)n+(a+b+c)}=(−1)^n n^2 3a=1 ⇒a=(1/3) 3a+2b=0 ⇒b=−(1/2) a+b+c=0 ⇒c=−(1/3)+(1/2)=(1/6) ⇒V_(n+1) +V_n =0 ⇒V_(n+1) =−V_n ⇒V_n =(−1)^n V_0 ⇒U_n =V_n +(−1)^(n−1) [(1/3)n^3 −(1/2)n^2 +(1/6)n] ⇒U_n =(−1)^n [V_0 −((n(n−1)(2n−1))/6)] assume U_0 =1, ⇒V_0 =U_0 =1 ⇒U_n =(−1)^n [1−((n(n−1)(2n−1))/6)] check: U_(n+1) =(−1)^(n+1) [1−(((n+1)n(2n+1))/6)] U_(n+1) =(−1)^n [−1+(((n+1)n(2n+1))/6)] U_(n+1) +U_n =(−1)^n [−((n(n−1)(2n−1))/6)+(((n+1)n(2n+1))/6)] U_(n+1) +U_n =(−1)^n n^2 ⇒ ok
$${say}\:{U}_{{n}} ={V}_{{n}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left[{an}^{\mathrm{3}} +{bn}^{\mathrm{2}} +{cn}\right] \\ $$$${U}_{{n}+\mathrm{1}} ={V}_{{n}+\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} \left[{a}\left({n}+\mathrm{1}\right)^{\mathrm{3}} +{b}\left({n}+\mathrm{1}\right)^{\mathrm{2}} +{c}\left({n}+\mathrm{1}\right)\right] \\ $$$${U}_{{n}+\mathrm{1}} +{U}_{{n}} ={V}_{{n}+\mathrm{1}} +{V}_{{n}} +\left(−\mathrm{1}\right)^{{n}} \left\{{a}\left[−{n}^{\mathrm{3}} +\left({n}+\mathrm{1}\right)^{\mathrm{3}} \right]+{b}\left[−{n}^{\mathrm{2}} +\left({n}+\mathrm{1}\right)^{\mathrm{2}} \right]+{c}\left[−{n}+\left({n}+\mathrm{1}\right)\right]\right\} \\ $$$${U}_{{n}+\mathrm{1}} +{U}_{{n}} ={V}_{{n}+\mathrm{1}} +{V}_{{n}} +\left(−\mathrm{1}\right)^{{n}} \left\{{a}\left[\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{1}\right]+{b}\left[\mathrm{2}{n}+\mathrm{1}\right]+{c}\right\} \\ $$$${U}_{{n}+\mathrm{1}} +{U}_{{n}} ={V}_{{n}+\mathrm{1}} +{V}_{{n}} +\left(−\mathrm{1}\right)^{{n}} \left\{\mathrm{3}{an}^{\mathrm{2}} +\left(\mathrm{3}{a}+\mathrm{2}{b}\right){n}+\left({a}+{b}+{c}\right)\right\}=\left(−\mathrm{1}\right)^{{n}} {n}^{\mathrm{2}} \\ $$$$\mathrm{3}{a}=\mathrm{1}\:\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{3}{a}+\mathrm{2}{b}=\mathrm{0}\:\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}+{b}+{c}=\mathrm{0}\:\Rightarrow{c}=−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow{V}_{{n}+\mathrm{1}} +{V}_{{n}} =\mathrm{0}\:\Rightarrow{V}_{{n}+\mathrm{1}} =−{V}_{{n}} \\ $$$$\Rightarrow{V}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {V}_{\mathrm{0}} \\ $$$$\Rightarrow{U}_{{n}} ={V}_{{n}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left[\frac{\mathrm{1}}{\mathrm{3}}{n}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{6}}{n}\right] \\ $$$$\Rightarrow{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \left[{V}_{\mathrm{0}} −\frac{{n}\left({n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}\right] \\ $$$${assume}\:{U}_{\mathrm{0}} =\mathrm{1},\:\Rightarrow{V}_{\mathrm{0}} ={U}_{\mathrm{0}} =\mathrm{1} \\ $$$$\Rightarrow{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \left[\mathrm{1}−\frac{{n}\left({n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}\right] \\ $$$${check}: \\ $$$${U}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left[\mathrm{1}−\frac{\left({n}+\mathrm{1}\right){n}\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\right] \\ $$$${U}_{{n}+\mathrm{1}} =\left(−\mathrm{1}\right)^{{n}} \left[−\mathrm{1}+\frac{\left({n}+\mathrm{1}\right){n}\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\right] \\ $$$${U}_{{n}+\mathrm{1}} +{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} \left[−\frac{{n}\left({n}−\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}+\frac{\left({n}+\mathrm{1}\right){n}\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\right] \\ $$$${U}_{{n}+\mathrm{1}} +{U}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {n}^{\mathrm{2}} \:\Rightarrow\:{ok} \\ $$
Commented by mr W last updated on 10/Jan/20
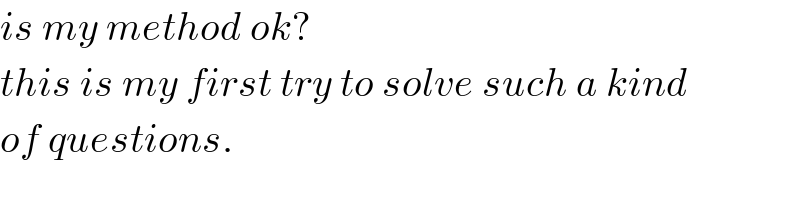
is my method ok? this is my first try to solve such a kind of questions.
$${is}\:{my}\:{method}\:{ok}? \\ $$$${this}\:{is}\:{my}\:{first}\:{try}\:{to}\:{solve}\:{such}\:{a}\:{kind} \\ $$$${of}\:{questions}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *