Menu Close

u-R-R-v-R-R-u-dv-dx-v-du-dx-

Tinku Tara
Pin




Question Number 297 by 123456 last updated on 25/Jan/15
u:R→R v:R→R { ((u=(dv/dx))),((v=(du/dx))) :}
$${u}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${v}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$$\begin{cases}{{u}=\frac{{dv}}{{dx}}}\\{{v}=\frac{{du}}{{dx}}}\end{cases} \\ $$
Answered by prakash jain last updated on 19/Dec/14
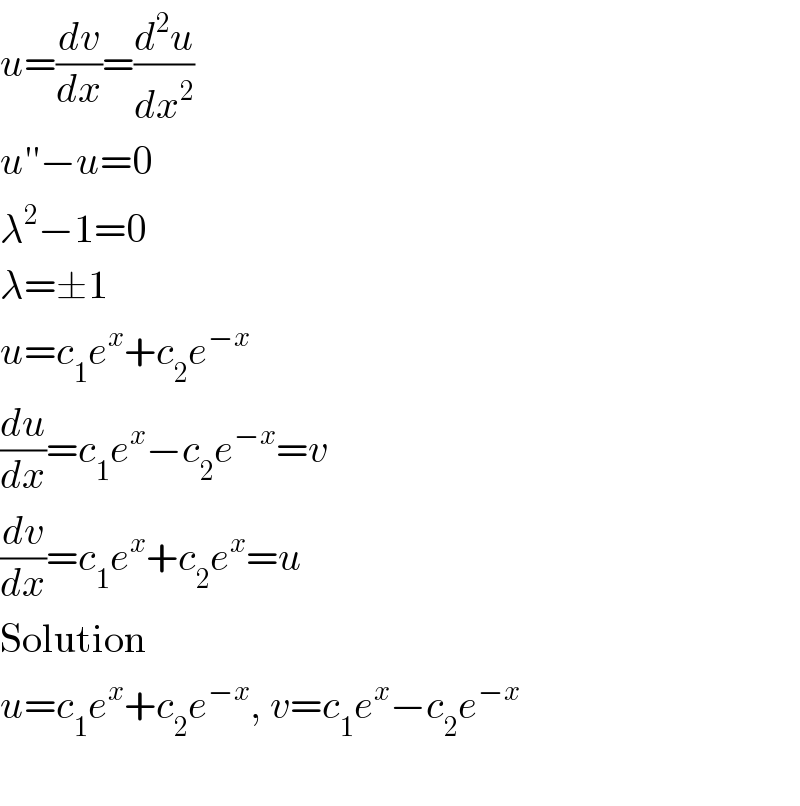
u=(dv/dx)=(d^2 u/dx^2 ) u′′−u=0 λ^2 −1=0 λ=±1 u=c_1 e^x +c_2 e^(−x) (du/dx)=c_1 e^x −c_2 e^(−x) =v (dv/dx)=c_1 e^x +c_2 e^x =u Solution u=c_1 e^x +c_2 e^(−x) , v=c_1 e^x −c_2 e^(−x)
$${u}=\frac{{dv}}{{dx}}=\frac{{d}^{\mathrm{2}} {u}}{{dx}^{\mathrm{2}} } \\ $$$${u}''−{u}=\mathrm{0} \\ $$$$\lambda^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\lambda=\pm\mathrm{1} \\ $$$${u}={c}_{\mathrm{1}} {e}^{{x}} +{c}_{\mathrm{2}} {e}^{−{x}} \\ $$$$\frac{{du}}{{dx}}={c}_{\mathrm{1}} {e}^{{x}} −{c}_{\mathrm{2}} {e}^{−{x}} ={v} \\ $$$$\frac{{dv}}{{dx}}={c}_{\mathrm{1}} {e}^{{x}} +{c}_{\mathrm{2}} {e}^{{x}} ={u} \\ $$$$\mathrm{Solution} \\ $$$${u}={c}_{\mathrm{1}} {e}^{{x}} +{c}_{\mathrm{2}} {e}^{−{x}} ,\:{v}={c}_{\mathrm{1}} {e}^{{x}} −{c}_{\mathrm{2}} {e}^{−{x}} \: \\ $$$$ \\ $$

Pin