Question Number 560 by 123456 last updated on 26/Jan/15
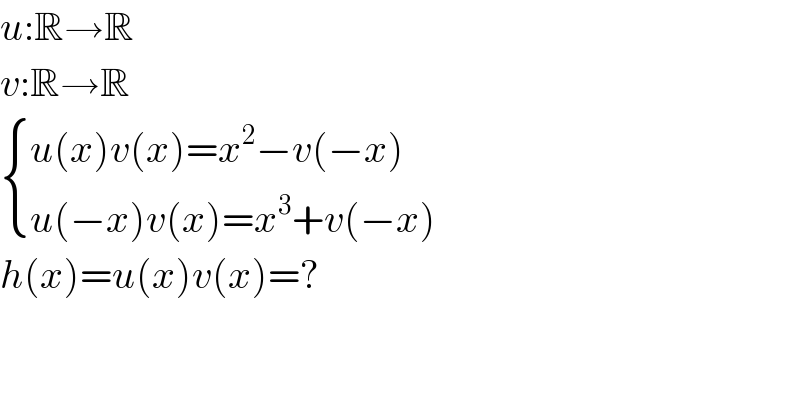
$${u}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${v}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$$\begin{cases}{{u}\left({x}\right){v}\left({x}\right)={x}^{\mathrm{2}} −{v}\left(−{x}\right)}\\{{u}\left(−{x}\right){v}\left({x}\right)={x}^{\mathrm{3}} +{v}\left(−{x}\right)}\end{cases} \\ $$$${h}\left({x}\right)={u}\left({x}\right){v}\left({x}\right)=? \\ $$
Answered by prakash jain last updated on 26/Jan/15
![u(x)v(x)=x^2 −v(−x) ...(i) u(−x)v(x)=x^3 +v(−x) ...(ii) add (i) and (ii) v(x)[u(x)+u(−x)]=x^2 +x^3 ⇒v(x)=((x^2 +x^3 )/(u(x)+u(−x))) u(−x)v(−x)=x^2 −v(x) replace x by −x in (i) u(−x)((x^2 −x^3 )/(u(x)+u(−x)))=x^2 −((x^2 +x^3 )/(u(x)+u(−x))) u(x)=a u(−x)=b ((b(x^2 −x^3 ))/(a+b))+((x^2 +x^3 )/(a+b))=x^2 bx^2 −bx^3 +x^2 +x^3 =ax^2 +bx^2 bx^3 =x^2 +x^3 −ax^2 b=((x^2 +x^3 −ax^2 )/x^3 )=((1+x−a)/x) 1+x−a=xb 1+x−u(x)=xu(−x) xu(−x)+u(x)−x−1=0 ...(iii) −xu(x)+u(−x)+x−1=0 ...(iv) replace x by −x in (iii) multiply (iv) by x −x^2 u(x)+xu(−x)+x^2 −x=0 ...(v) add (iii) and (v) u(x)+x^2 u(x)−x^2 −1=0 u(x)=1, u(−x)=1 v(x)=((x^2 +x^3 )/2), v(−x)=((x^2 −x^3 )/2) Check condition 1 u(x)v(x)=((x^2 +x^3 )/2)=x^2 −((x^2 −x^3 )/2)=((x^2 +x^3 )/2) Check condition 1 u(−x)v(x)=((x^2 +x^3 )/2)=x^3 +((x^2 −x^3 )/2)=((x^2 +x^3 )/2) Results u(x)=1 v(x)=((x^2 +x^3 )/2) u(x)v(x)=((x^2 +x^3 )/2)](https://www.tinkutara.com/question/Q564.png)
$${u}\left({x}\right){v}\left({x}\right)={x}^{\mathrm{2}} −{v}\left(−{x}\right)\:\:\:\:\:…\left(\mathrm{i}\right) \\ $$$${u}\left(−{x}\right){v}\left({x}\right)={x}^{\mathrm{3}} +{v}\left(−{x}\right)\:\:…\left(\mathrm{ii}\right) \\ $$$$\mathrm{add}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right) \\ $$$${v}\left({x}\right)\left[{u}\left({x}\right)+{u}\left(−{x}\right)\right]={x}^{\mathrm{2}} +{x}^{\mathrm{3}} \Rightarrow{v}\left({x}\right)=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{{u}\left({x}\right)+{u}\left(−{x}\right)} \\ $$$${u}\left(−{x}\right){v}\left(−{x}\right)={x}^{\mathrm{2}} −{v}\left({x}\right)\:\mathrm{replace}\:{x}\:\mathrm{by}\:−{x}\:\mathrm{in}\:\left(\mathrm{i}\right) \\ $$$${u}\left(−{x}\right)\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }{{u}\left({x}\right)+{u}\left(−{x}\right)}={x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{{u}\left({x}\right)+{u}\left(−{x}\right)} \\ $$$${u}\left({x}\right)={a} \\ $$$${u}\left(−{x}\right)={b} \\ $$$$\frac{{b}\left({x}^{\mathrm{2}} −{x}^{\mathrm{3}} \right)}{{a}+{b}}+\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{{a}+{b}}={x}^{\mathrm{2}} \\ $$$${bx}^{\mathrm{2}} −{bx}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}^{\mathrm{3}} ={ax}^{\mathrm{2}} +{bx}^{\mathrm{2}} \\ $$$${bx}^{\mathrm{3}} ={x}^{\mathrm{2}} +{x}^{\mathrm{3}} −{ax}^{\mathrm{2}} \\ $$$${b}=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} −{ax}^{\mathrm{2}} }{{x}^{\mathrm{3}} }=\frac{\mathrm{1}+{x}−{a}}{{x}} \\ $$$$\mathrm{1}+{x}−{a}={xb} \\ $$$$\mathrm{1}+{x}−{u}\left({x}\right)={xu}\left(−{x}\right) \\ $$$${xu}\left(−{x}\right)+{u}\left({x}\right)−{x}−\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\:…\left(\mathrm{iii}\right) \\ $$$$−{xu}\left({x}\right)+{u}\left(−{x}\right)+{x}−\mathrm{1}=\mathrm{0}\:\:\:\:…\left(\mathrm{iv}\right)\:\mathrm{replace}\:{x}\:\mathrm{by}\:−{x}\:\mathrm{in}\:\left(\mathrm{iii}\right) \\ $$$$\mathrm{multiply}\:\left(\mathrm{iv}\right)\:\mathrm{by}\:{x} \\ $$$$−{x}^{\mathrm{2}} {u}\left({x}\right)+{xu}\left(−{x}\right)+{x}^{\mathrm{2}} −{x}=\mathrm{0}\:\:\:\:\:\:…\left(\mathrm{v}\right) \\ $$$$\mathrm{add}\:\left(\mathrm{iii}\right)\:\mathrm{and}\:\left(\mathrm{v}\right) \\ $$$${u}\left({x}\right)+{x}^{\mathrm{2}} {u}\left({x}\right)−{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${u}\left({x}\right)=\mathrm{1},\:{u}\left(−{x}\right)=\mathrm{1} \\ $$$${v}\left({x}\right)=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{\mathrm{2}},\:{v}\left(−{x}\right)=\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$$${Check}\:{condition}\:\mathrm{1} \\ $$$${u}\left({x}\right){v}\left({x}\right)=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{\mathrm{2}}={x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }{\mathrm{2}}=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$$${Check}\:{condition}\:\mathrm{1} \\ $$$${u}\left(−{x}\right){v}\left({x}\right)=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{\mathrm{2}}={x}^{\mathrm{3}} +\frac{{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }{\mathrm{2}}=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$$$\mathrm{Results} \\ $$$${u}\left({x}\right)=\mathrm{1} \\ $$$${v}\left({x}\right)=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$$${u}\left({x}\right){v}\left({x}\right)=\frac{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$
