Menu Close

u-x-cosh-x-x-v-n-1-u-v-n-m-2-ln-1-2-v-0-1-A-V-n-V-0-nm-B-v-n-v-0-nm-2-lim-n-v-n-

Tinku Tara
Pin




Question Number 131132 by 676597498 last updated on 01/Feb/21
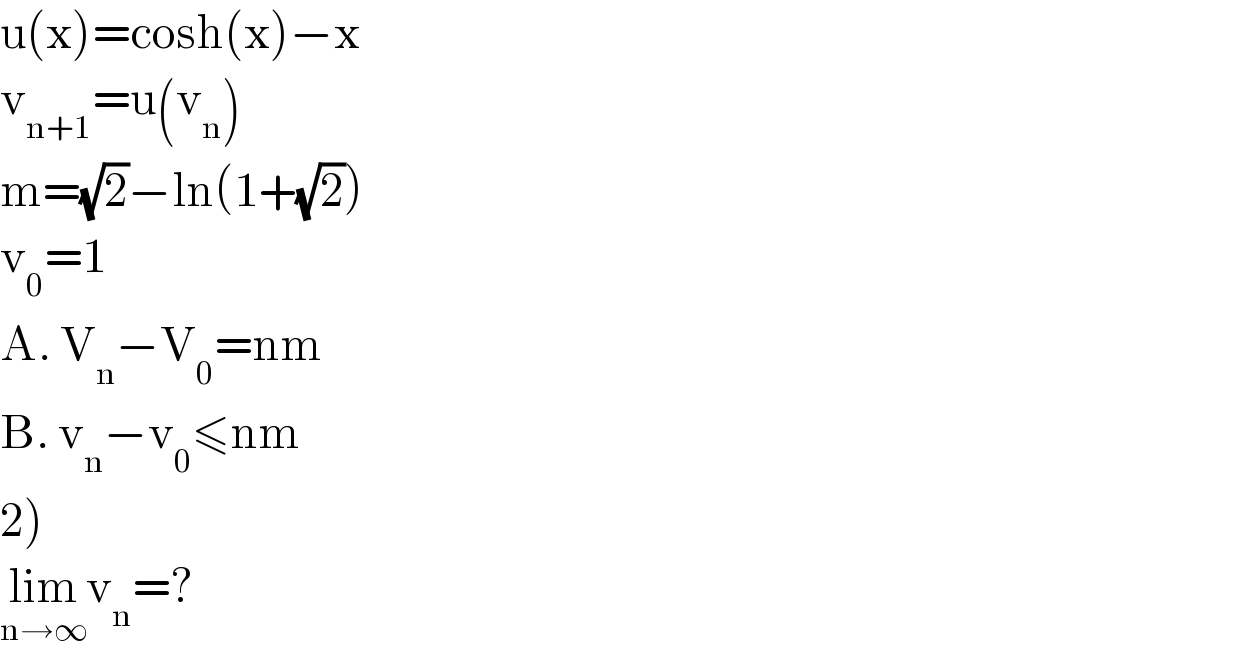
u(x)=cosh(x)−x v_(n+1) =u(v_n ) m=(√2)−ln(1+(√2)) v_0 =1 A. V_n −V_0 =nm B. v_n −v_0 ≤nm 2) lim_(n→∞) v_n =?
$$\mathrm{u}\left(\mathrm{x}\right)=\mathrm{cosh}\left(\mathrm{x}\right)−\mathrm{x} \\ $$$$\mathrm{v}_{\mathrm{n}+\mathrm{1}} =\mathrm{u}\left(\mathrm{v}_{\mathrm{n}} \right) \\ $$$$\mathrm{m}=\sqrt{\mathrm{2}}−\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$\mathrm{v}_{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{A}.\:\mathrm{V}_{\mathrm{n}} −\mathrm{V}_{\mathrm{0}} =\mathrm{nm} \\ $$$$\mathrm{B}.\:\mathrm{v}_{\mathrm{n}} −\mathrm{v}_{\mathrm{0}} \leqslant\mathrm{nm} \\ $$$$\left.\mathrm{2}\right) \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}v}_{\mathrm{n}} =? \\ $$

Pin