Menu Close

unsolved-question-0-cos-x-2-cos-x-dx-x-2-

Tinku Tara 0 Comments
Pin




Question Number 136966 by Ñï= last updated on 28/Mar/21
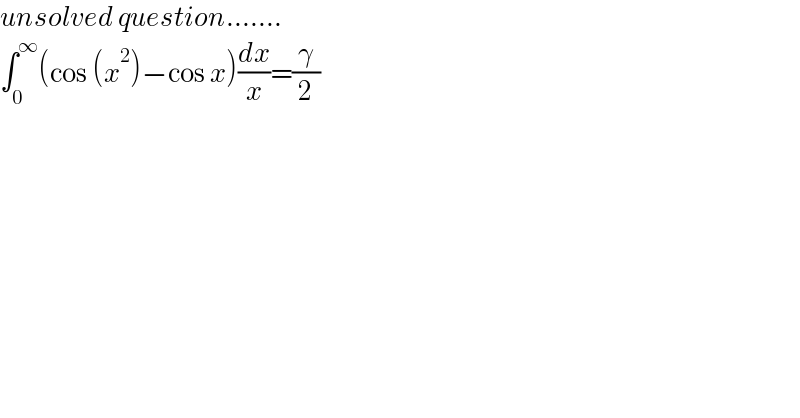
unsolved question....... ∫_0 ^∞ (cos (x^2 )−cos x)(dx/x)=(γ/2)
$${unsolved}\:{question}……. \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\mathrm{cos}\:\left({x}^{\mathrm{2}} \right)−\mathrm{cos}\:{x}\right)\frac{{dx}}{{x}}=\frac{\gamma}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 29/Mar/21
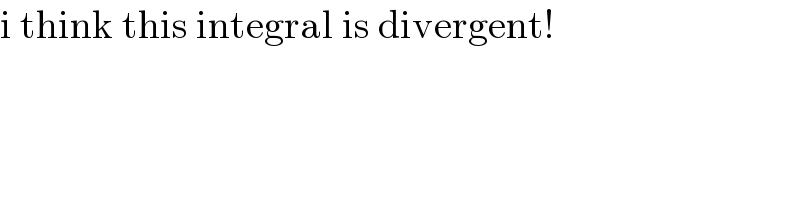
i think this integral is divergent!
$$\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{divergent}! \\ $$
Commented by Ñï= last updated on 29/Mar/21
I(a,p)=∫_0 ^∞ x^p (((sin (ax^2 ))/x^2 )−((sin (ax))/x))dx=∫_0 ^∞ x^(p−2) sin (ax^2 )dx−∫_0 ^∞ x^(p−1) sin (ax)dx =(1/2)∫_0 ^∞ u^((p/2)−(3/2)) sin (au)du−∫_0 ^∞ x^(p−1) sin (ax)dx =(1/2)M_(((p/2)−(1/2),x)) (sin (ax))−M_((p,x)) (sin (ax)) M_((p,x)) (sin (ax))=a^(−p) M_((p,x)) (sin x)=a^(−p) Γ(p)sin (((pπ)/2)) I(a,p)=(1/2)a^(−(p/2)+(1/2)) Γ(((p−1)/2))sin ((π/2)(((p−1)/2)))−a^(−p) Γ(p)sin (((pπ)/2)) ;(p>−1,a>0) ∫_0 ^∞ (cos (x^2 )−cos x)(dx/x)=lim_(p→−1) lim_(a→1) ((dI(a,p))/da) =lim_(p→−1) lim_(a→1) (1/2)a^(−p−1) {−a^((p+1)/2) sin (((p−1)/4)π)Γ(((p+1)/2))+2sin (((pπ)/2))Γ(p+1)} =lim_(p→−1) (1/2){−sin (((p−1)/4)π)Γ(((p+1)/2))+2sin (((pπ)/2))Γ(p+1)} =lim_(p→−1) (1/2){−sin (((p−1)/4)π)((2/(p+1))−γ+o(1))+2sin (((pπ)/2))((1/(p+1))−γ+o(1))} =(1/2)(−γ+2γ)=(γ/2) I still dont understand ∙∙∙,Expect for Mr 1970′s answer, after all,he gives this question.
$${I}\left({a},{p}\right)=\int_{\mathrm{0}} ^{\infty} {x}^{{p}} \left(\frac{\mathrm{sin}\:\left({ax}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }−\frac{\mathrm{sin}\:\left({ax}\right)}{{x}}\right){dx}=\int_{\mathrm{0}} ^{\infty} {x}^{{p}−\mathrm{2}} \mathrm{sin}\:\left({ax}^{\mathrm{2}} \right){dx}−\int_{\mathrm{0}} ^{\infty} {x}^{{p}−\mathrm{1}} \mathrm{sin}\:\left({ax}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {u}^{\frac{{p}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{sin}\:\left({au}\right){du}−\int_{\mathrm{0}} ^{\infty} {x}^{{p}−\mathrm{1}} \mathrm{sin}\:\left({ax}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathcal{M}_{\left(\frac{{p}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}},{x}\right)} \left(\mathrm{sin}\:\left({ax}\right)\right)−\mathcal{M}_{\left({p},{x}\right)} \left(\mathrm{sin}\:\left({ax}\right)\right) \\ $$$$\mathcal{M}_{\left({p},{x}\right)} \left(\mathrm{sin}\:\left({ax}\right)\right)={a}^{−{p}} \mathcal{M}_{\left({p},{x}\right)} \left(\mathrm{sin}\:{x}\right)={a}^{−{p}} \Gamma\left({p}\right)\mathrm{sin}\:\left(\frac{{p}\pi}{\mathrm{2}}\right) \\ $$$${I}\left({a},{p}\right)=\frac{\mathrm{1}}{\mathrm{2}}{a}^{−\frac{{p}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}} \Gamma\left(\frac{{p}−\mathrm{1}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\left(\frac{{p}−\mathrm{1}}{\mathrm{2}}\right)\right)−{a}^{−{p}} \Gamma\left({p}\right)\mathrm{sin}\:\left(\frac{{p}\pi}{\mathrm{2}}\right)\:\:\:\:\:;\left({p}>−\mathrm{1},{a}>\mathrm{0}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\mathrm{cos}\:\left({x}^{\mathrm{2}} \right)−\mathrm{cos}\:{x}\right)\frac{{dx}}{{x}}=\underset{{p}\rightarrow−\mathrm{1}} {\mathrm{lim}}\underset{{a}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{dI}\left({a},{p}\right)}{{da}} \\ $$$$=\underset{{p}\rightarrow−\mathrm{1}} {\mathrm{lim}}\underset{{a}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}}{a}^{−{p}−\mathrm{1}} \left\{−{a}^{\frac{{p}+\mathrm{1}}{\mathrm{2}}} \mathrm{sin}\:\left(\frac{{p}−\mathrm{1}}{\mathrm{4}}\pi\right)\Gamma\left(\frac{{p}+\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2sin}\:\left(\frac{{p}\pi}{\mathrm{2}}\right)\Gamma\left({p}+\mathrm{1}\right)\right\} \\ $$$$=\underset{{p}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{sin}\:\left(\frac{{p}−\mathrm{1}}{\mathrm{4}}\pi\right)\Gamma\left(\frac{{p}+\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2sin}\:\left(\frac{{p}\pi}{\mathrm{2}}\right)\Gamma\left({p}+\mathrm{1}\right)\right\} \\ $$$$=\underset{{p}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}}\left\{−\mathrm{sin}\:\left(\frac{{p}−\mathrm{1}}{\mathrm{4}}\pi\right)\left(\frac{\mathrm{2}}{{p}+\mathrm{1}}−\gamma+{o}\left(\mathrm{1}\right)\right)+\mathrm{2sin}\:\left(\frac{{p}\pi}{\mathrm{2}}\right)\left(\frac{\mathrm{1}}{{p}+\mathrm{1}}−\gamma+{o}\left(\mathrm{1}\right)\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(−\gamma+\mathrm{2}\gamma\right)=\frac{\gamma}{\mathrm{2}} \\ $$$${I}\:{still}\:\:{dont}\:{understand}\:\centerdot\centerdot\centerdot,{Expect}\:{for}\:{Mr}\:\mathrm{1970}'{s}\:{answer}, \\ $$$${after}\:{all},{he}\:{gives}\:{this}\:{question}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *