Menu Close

Use-De-Moivre-s-theorem-to-prove-that-r-0-cos-rx-1-2-and-find-a-value-or-expression-for-r-0-sin-rx-assume-that-this-two-series-were-convergent-

Tinku Tara 0 Comments
Pin




Question Number 136582 by physicstutes last updated on 23/Mar/21
Use De′Moivre′s theorem to prove that Σ_(r=0) ^∞ cos rx = (1/2) and find a value(or expression) for Σ_(r=0) ^∞ sin rx assume that this two series were convergent.
$$\mathrm{Use}\:\mathrm{De}'\mathrm{Moivre}'\mathrm{s}\:\mathrm{theorem}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\:\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{cos}\:{rx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{find}\:\mathrm{a}\:\mathrm{value}\left(\mathrm{or}\:\mathrm{expression}\right)\:\mathrm{for}\:\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{sin}\:{rx} \\ $$$$\mathrm{assume}\:\mathrm{that}\:\mathrm{this}\:\mathrm{two}\:\mathrm{series}\:\mathrm{were}\:\mathrm{convergent}. \\ $$
Answered by Ar Brandon last updated on 23/Mar/21
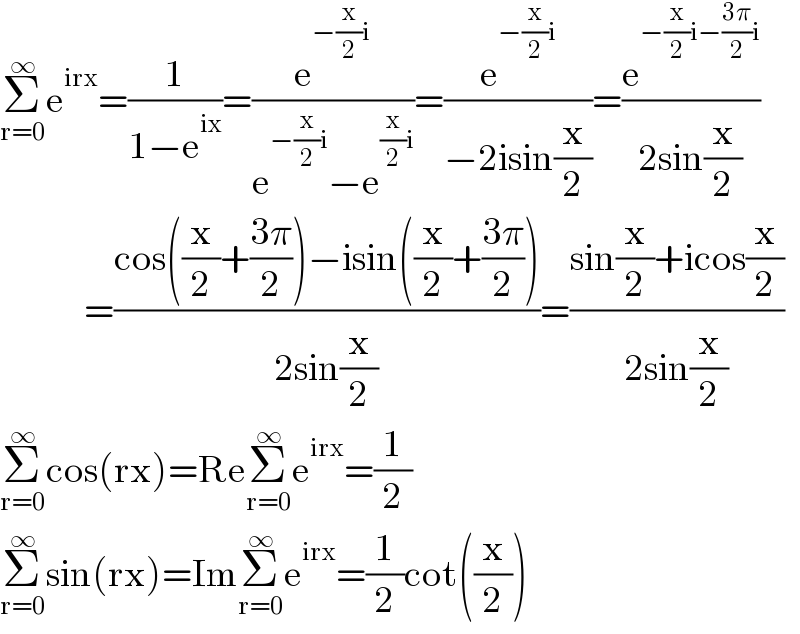
Σ_(r=0) ^∞ e^(irx) =(1/(1−e^(ix) ))=(e^(−(x/2)i) /(e^(−(x/2)i) −e^((x/2)i) ))=(e^(−(x/2)i) /(−2isin(x/2)))=(e^(−(x/2)i−((3π)/2)i) /(2sin(x/2))) =((cos((x/2)+((3π)/2))−isin((x/2)+((3π)/2)))/(2sin(x/2)))=((sin(x/2)+icos(x/2))/(2sin(x/2))) Σ_(r=0) ^∞ cos(rx)=ReΣ_(r=0) ^∞ e^(irx) =(1/2) Σ_(r=0) ^∞ sin(rx)=ImΣ_(r=0) ^∞ e^(irx) =(1/2)cot((x/2))
$$\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{e}^{\mathrm{irx}} =\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{\mathrm{ix}} }=\frac{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{i}} }{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{i}} −\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}\mathrm{i}} }=\frac{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{i}} }{−\mathrm{2isin}\frac{\mathrm{x}}{\mathrm{2}}}=\frac{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{i}−\frac{\mathrm{3}\pi}{\mathrm{2}}\mathrm{i}} }{\mathrm{2sin}\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{3}\pi}{\mathrm{2}}\right)−\mathrm{isin}\left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{3}\pi}{\mathrm{2}}\right)}{\mathrm{2sin}\frac{\mathrm{x}}{\mathrm{2}}}=\frac{\mathrm{sin}\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{icos}\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{2sin}\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{cos}\left(\mathrm{rx}\right)=\mathrm{Re}\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{e}^{\mathrm{irx}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{sin}\left(\mathrm{rx}\right)=\mathrm{Im}\underset{\mathrm{r}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{e}^{\mathrm{irx}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cot}\left(\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$
Commented by physicstutes last updated on 23/Mar/21
perfect
$$\mathrm{perfect} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *