Question Number 1499 by 112358 last updated on 14/Aug/15

Commented by 123456 last updated on 14/Aug/15

Commented by 123456 last updated on 14/Aug/15
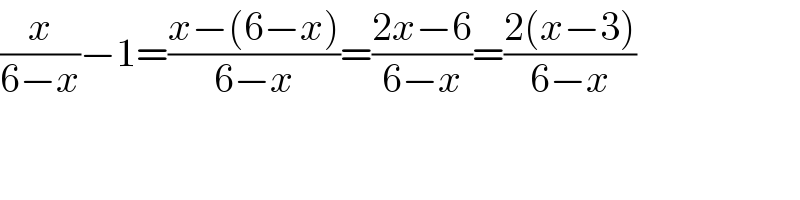
Commented by 123456 last updated on 14/Aug/15

Answered by 123456 last updated on 16/Aug/15

