Menu Close

use-trigonometric-substitution-to-solve-x-3-9-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 142116 by Eric002 last updated on 26/May/21
use trigonometric substitution to solve ∫(x^3 /( (√(9−x^2 ))))dx
usetrigonometricsubstitutiontosolve∫x39−x2dx
Answered by ZiYangLee last updated on 27/May/21
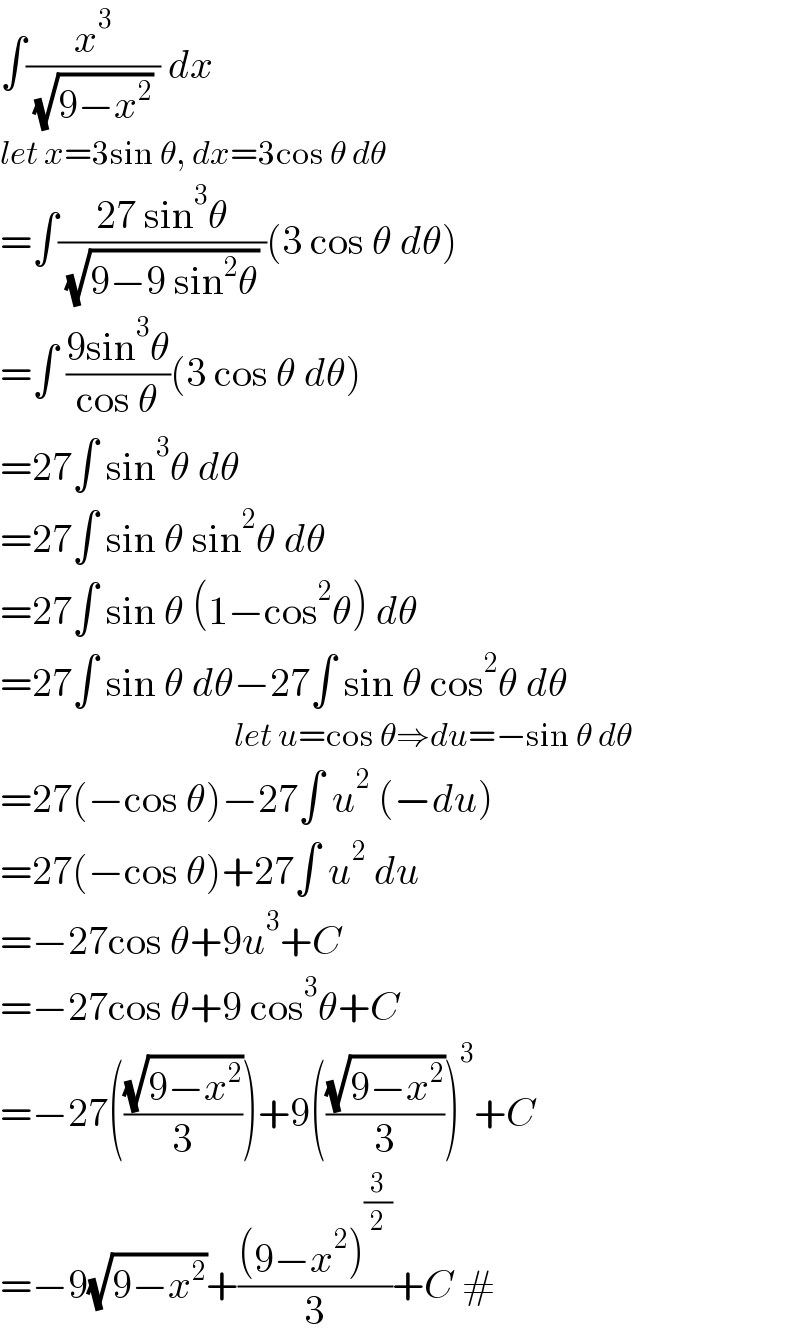
∫(x^3 /( (√(9−x^2 )) )) dx let x=3sin θ, dx=3cos θ dθ =∫((27 sin^3 θ)/( (√(9−9 sin^2 θ)) ))(3 cos θ dθ) =∫ ((9sin^3 θ)/(cos θ))(3 cos θ dθ) =27∫ sin^3 θ dθ =27∫ sin θ sin^2 θ dθ =27∫ sin θ (1−cos^2 θ) dθ =27∫ sin θ dθ−27∫ sin θ cos^2 θ dθ let u=cos θ⇒du=−sin θ dθ =27(−cos θ)−27∫ u^2 (−du) =27(−cos θ)+27∫ u^2 du =−27cos θ+9u^3 +C =−27cos θ+9 cos^3 θ+C =−27(((√(9−x^2 ))/3))+9(((√(9−x^2 ))/3))^3 +C =−9(√(9−x^2 ))+(((9−x^2 )^(3/2) )/3)+C #
∫x39−x2dxletx=3sinθ,dx=3cosθdθ=∫27sin3θ9−9sin2θ(3cosθdθ)=∫9sin3θcosθ(3cosθdθ)=27∫sin3θdθ=27∫sinθsin2θdθ=27∫sinθ(1−cos2θ)dθ=27∫sinθdθ−27∫sinθcos2θdθletu=cosθ⇒du=−sinθdθ=27(−cosθ)−27∫u2(−du)=27(−cosθ)+27∫u2du=−27cosθ+9u3+C=−27cosθ+9cos3θ+C=−27(9−x23)+9(9−x23)3+CYou can't use 'macro parameter character #' in math mode
Answered by mathmax by abdo last updated on 27/May/21
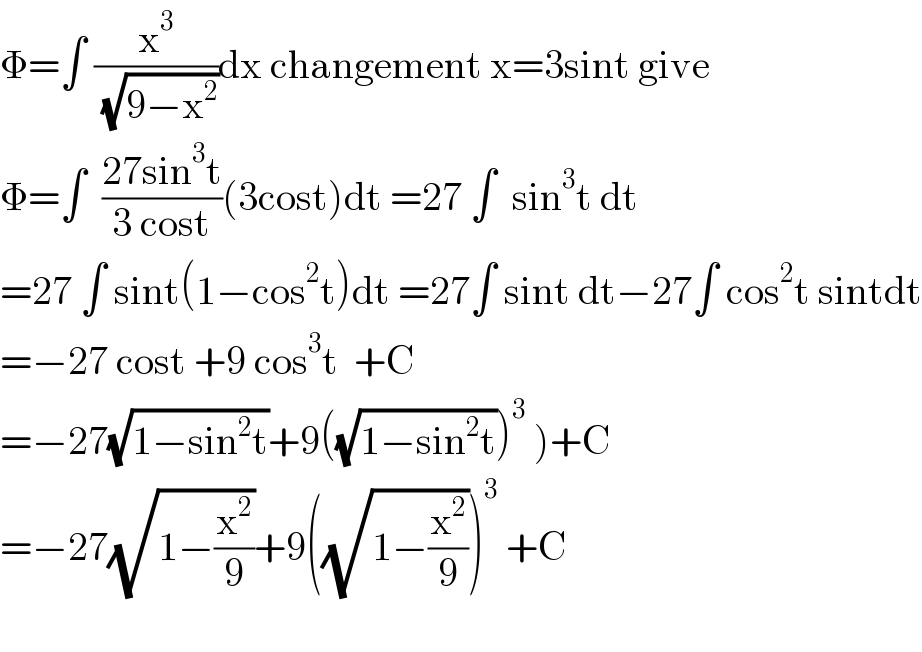
Φ=∫ (x^3 /( (√(9−x^2 ))))dx changement x=3sint give Φ=∫ ((27sin^3 t)/(3 cost))(3cost)dt =27 ∫ sin^3 t dt =27 ∫ sint(1−cos^2 t)dt =27∫ sint dt−27∫ cos^2 t sintdt =−27 cost +9 cos^3 t +C =−27(√(1−sin^2 t))+9((√(1−sin^2 t)))^3 )+C =−27(√(1−(x^2 /9)))+9((√(1−(x^2 /9))))^3 +C
Φ=∫x39−x2dxchangementx=3sintgiveΦ=∫27sin3t3cost(3cost)dt=27∫sin3tdt=27∫sint(1−cos2t)dt=27∫sintdt−27∫cos2tsintdt=−27cost+9cos3t+C=−271−sin2t+9(1−sin2t)3)+C=−271−x29+9(1−x29)3+C

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *