Question Number 133277 by Engr_Jidda last updated on 20/Feb/21
![use weierstrass m−test and dirichlet test to confirm the uniformly covergence of the following series in the interval [0,1] a) Σ_(n=1) ^∞ ((cosnx)/n^4 ) b) Σ_(n=1) ^∞ ((cosnx)/n^(8/7) ) c) Σ_(n=1) ^∞ (x^n /n^(3/2) ) d) Σ_(n=1) ^∞ (1/(n^2 +x^2 ))](https://www.tinkutara.com/question/Q133277.png)
$${use}\:{weierstrass}\:{m}−{test}\:{and}\:{dirichlet} \\ $$$${test}\:{to}\:{confirm}\:{the}\:{uniformly}\:{covergence} \\ $$$${of}\:{the}\:{following}\:{series}\:{in}\:{the}\:{interval}\:\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\left.{a}\right)\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cosnx}}{{n}^{\mathrm{4}} } \\ $$$$\left.{b}\right)\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cosnx}}{{n}^{\frac{\mathrm{8}}{\mathrm{7}}} } \\ $$$$ \\ $$$$\left.{c}\right)\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{x}^{{n}} }{{n}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$ \\ $$$$\left.{d}\right)\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 21/Feb/21
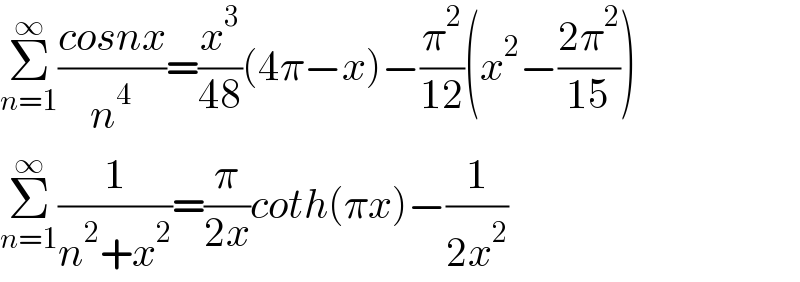
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cosnx}}{{n}^{\mathrm{4}} }=\frac{{x}^{\mathrm{3}} }{\mathrm{48}}\left(\mathrm{4}\pi−{x}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\left({x}^{\mathrm{2}} −\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{15}}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}{x}}{coth}\left(\pi{x}\right)−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$
Commented by Engr_Jidda last updated on 22/Feb/21

$${thank}\:{you}\:{sir} \\ $$
