V-ln-x-1-x-2-dx-

Question Number 133951 by liberty last updated on 25/Feb/21

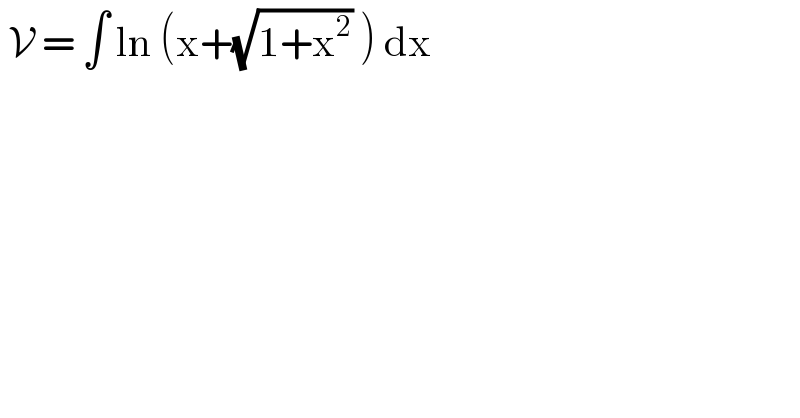
$$\:\mathcal{V}\:=\:\int\:\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\right)\:\mathrm{dx}\: \\ $$

Answered by mathmax by abdo last updated on 25/Feb/21

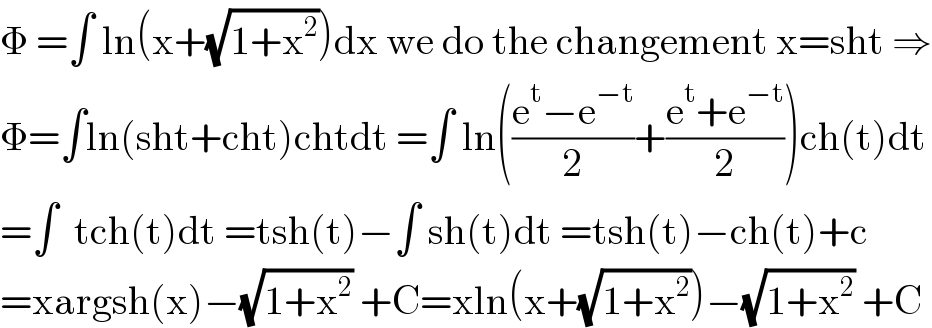
Φ =∫ ln(x+(√(1+x^2 )))dx we do the changement x=sht ⇒ Φ=∫ln(sht+cht)chtdt =∫ ln(((e^t −e^(−t) )/2)+((e^t +e^(−t) )/2))ch(t)dt =∫ tch(t)dt =tsh(t)−∫ sh(t)dt =tsh(t)−ch(t)+c =xargsh(x)−(√(1+x^2 )) +C=xln(x+(√(1+x^2 )))−(√(1+x^2 )) +C

$$\Phi\:=\int\:\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{sht}\:\Rightarrow \\ $$$$\Phi=\int\mathrm{ln}\left(\mathrm{sht}+\mathrm{cht}\right)\mathrm{chtdt}\:=\int\:\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}+\frac{\mathrm{e}^{\mathrm{t}} +\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}\right)\mathrm{ch}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int\:\:\mathrm{tch}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{tsh}\left(\mathrm{t}\right)−\int\:\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{tsh}\left(\mathrm{t}\right)−\mathrm{ch}\left(\mathrm{t}\right)+\mathrm{c} \\ $$$$=\mathrm{xargsh}\left(\mathrm{x}\right)−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\mathrm{C}=\mathrm{xln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\mathrm{C} \\ $$

Answered by bobhans last updated on 26/Feb/21

integration by parts { ((u=ln (x+(√(1+x^2 )) )→du=((1+(x/( (√(1+x^2 )))))/(x+(√(1+x^2 )))) dx)),((v = x)) :} I=xln (x+(√(1+x^2 )))−∫x(((x+(√(1+x^2 )))/((x+(√(1+x^2 )))(√(1+x^2 )))))dx I=xln (x+(√(1+x^2 )))−∫ (x/( (√(1+x^2 )))) dx I=xln (x+(√(1+x^2 )))−(1/2)∫ ((d(1+x^2 ))/( (√(1+x^2 )))) I=x ln (x+(√(1+x^2 )) )−(√(1+x^2 )) + c

$$\mathrm{integration}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\begin{cases}{\mathrm{u}=\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\right)\rightarrow\mathrm{du}=\frac{\mathrm{1}+\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}}{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}}\\{\mathrm{v}\:=\:\mathrm{x}}\end{cases} \\ $$$$\mathrm{I}=\mathrm{xln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\int\mathrm{x}\left(\frac{\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right)\mathrm{dx} \\ $$$$\mathrm{I}=\mathrm{xln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\int\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx} \\ $$$$\mathrm{I}=\mathrm{xln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{I}=\mathrm{x}\:\mathrm{ln}\:\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\right)−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\:\mathrm{c}\: \\ $$

Answered by physicstutes last updated on 26/Feb/21

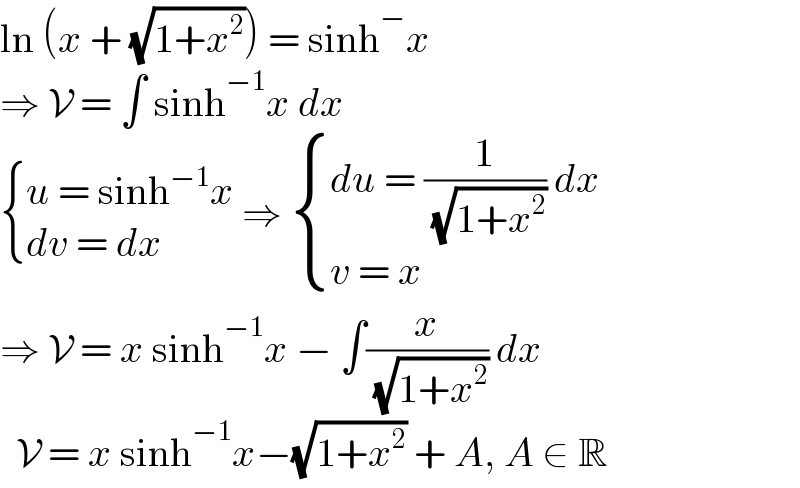
ln (x + (√(1+x^2 ))) = sinh^− x ⇒ V = ∫ sinh^(−1) x dx { ((u = sinh^(−1) x)),((dv = dx)) :} ⇒ { ((du = (1/( (√(1+x^2 )))) dx)),((v = x)) :} ⇒ V = x sinh^(−1) x − ∫(x/( (√(1+x^2 )))) dx V = x sinh^(−1) x−(√(1+x^2 )) + A, A ∈ R

$$\mathrm{ln}\:\left({x}\:+\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:=\:\mathrm{sinh}^{−} {x} \\ $$$$\Rightarrow\:\mathcal{V}\:=\:\int\:\mathrm{sinh}^{−\mathrm{1}} {x}\:{dx} \\ $$$$\begin{cases}{{u}\:=\:\mathrm{sinh}^{−\mathrm{1}} {x}}\\{{dv}\:=\:{dx}}\end{cases}\:\Rightarrow\:\begin{cases}{{du}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}}\\{{v}\:=\:{x}}\end{cases} \\ $$$$\Rightarrow\:\mathcal{V}\:=\:{x}\:\mathrm{sinh}^{−\mathrm{1}} {x}\:−\:\int\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$$$\:\:\mathcal{V}\:=\:{x}\:\mathrm{sinh}^{−\mathrm{1}} {x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\:{A},\:{A}\:\in\:\mathbb{R} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply